Current status and prospects of calculation methods for dam and dike failures (Ⅰ):Theoretical models, parameter models, and one-dimensional mathematical models
-
摘要:
国内外堤坝溃决事故屡有发生,堤坝安全对防范洪水灾害至关重要。溃口发展机理及数学计算模型的研究对于洪水预测与风险防范具有重要意义。以溃口数学计算模型的发展脉络为主线,对堤坝溃口特性及溃决过程进行了概括总结,并基于堤坝溃口类型与影响因素的分析,对其分类与演化规律进行了归纳梳理,对比已有模型试验结果与数学计算模型的关系。按照理论模型、参数模型和一维数学模型的演进路径,对堤坝溃决计算方法进行了全面综述,系统汇总了溃口数学模型的历史发展与研究现状,并对不同数学模型的特征和适用性进行了简要比较。以表格形式列举了常见溃口计算方法,便于学者查阅与模型对比,进一步把握溃口发展数学模型的研究方向。总体而言,理论模型与参数模型因计算简便,可快速应用于溃决应急与抢险,但难以描述溃口的动态演化;一维数学模型能够耦合复杂的水流运动、溃口几何变化与泥沙输移过程,更为精细地刻画堤坝溃决的动态特征,但仍存在物理过程简化与假设较多的问题。随着二维、三维数学模型的发展,以及机器学习与人工智能方法的引入,溃口计算模型正朝着物理过程刻画更为精细、计算效率更高的方向演进。
Abstract:Significance Dam and dike failures occur frequently worldwide, and embankment safety is crucial for flood prevention and disaster mitigation. Research on breach development mechanisms and mathematical models is of great significance for flood forecasting and risk prevention.
Progress Following the developmental context of breach mathematical models, this paper summarizes the characteristics and processes of dam breaches, analyzes breach types and influencing factors, summarizes their classification and evolutionary patterns, and compares the relationship between model test results and mathematical models. Theoretical models, parameter models, and one-dimensional mathematical models are systematically reviewed to summarize the historical evolution and current state of dam breach modeling. The distinct features and applicability of different modeling approaches are comparatively analyzed, and common breach calculation methods are summarized in a table to facilitate model reference and comparison, thereby providing a clearer understanding of research directions in mathematical models of breach development.
Conclusion and Prospect In general, theoretical and parameter models are computationally simple and can be quickly applied to emergency breach assessment and disaster response, yet they fail to capture the dynamic evolution of the breach process. One-dimensional mathematical models, by incorporating complex hydraulic flow, breach geometry variation, and sediment transport, provide more detailed representations of breach dynamics, though they still rely on simplifications and assumptions of physical processes. With the rapid advancement of two- and three-dimensional mathematical models, as well as the introduction of machine learning and artificial intelligence techniques, breach modeling is evolving toward more refined physical representation and higher computational efficiency.
-
Key words:
- dam and dike /
- breach development /
- theoretical model /
- parameter model /
- mathematical model
-
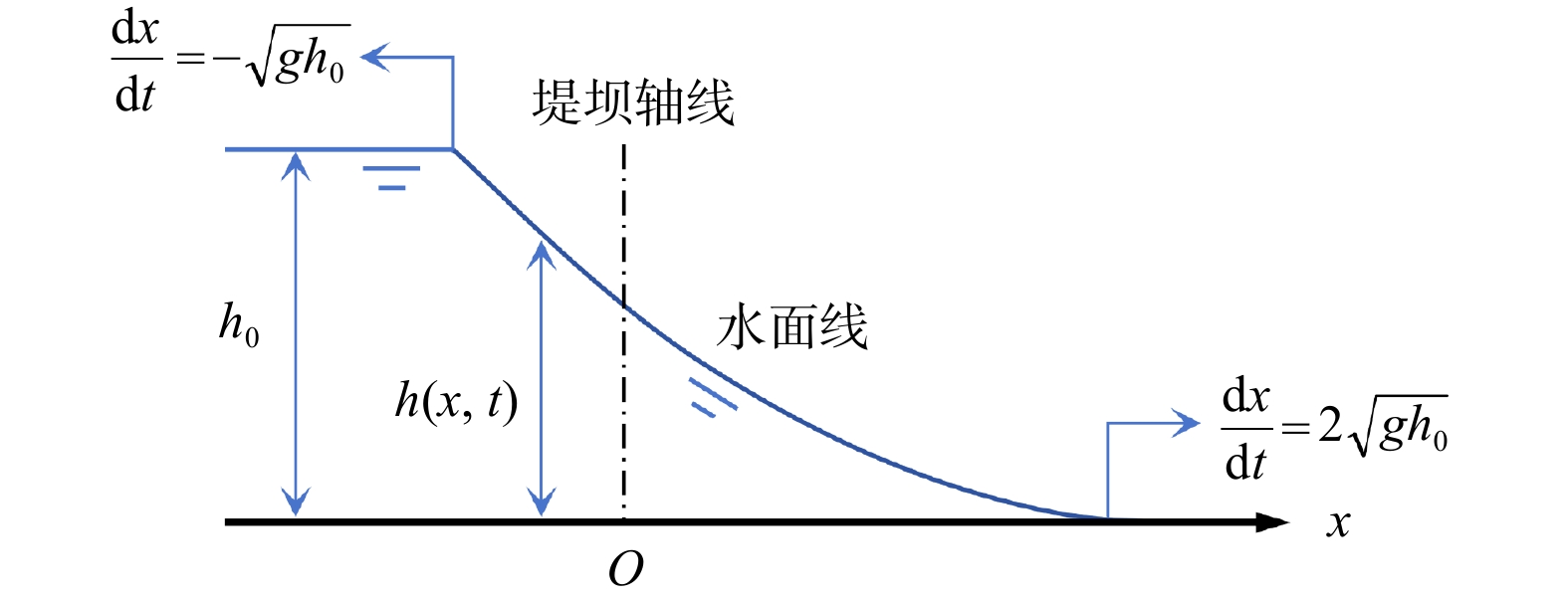
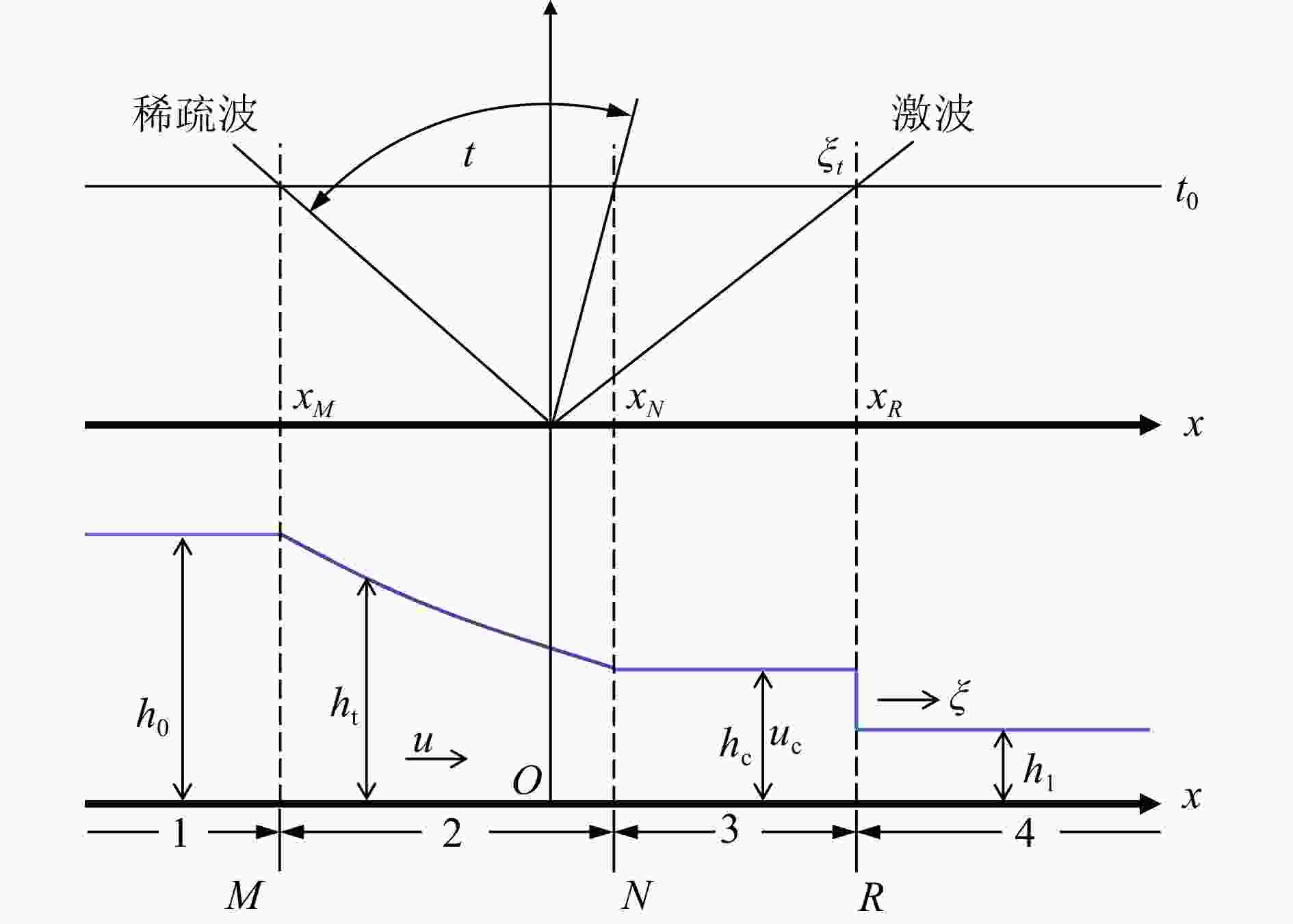
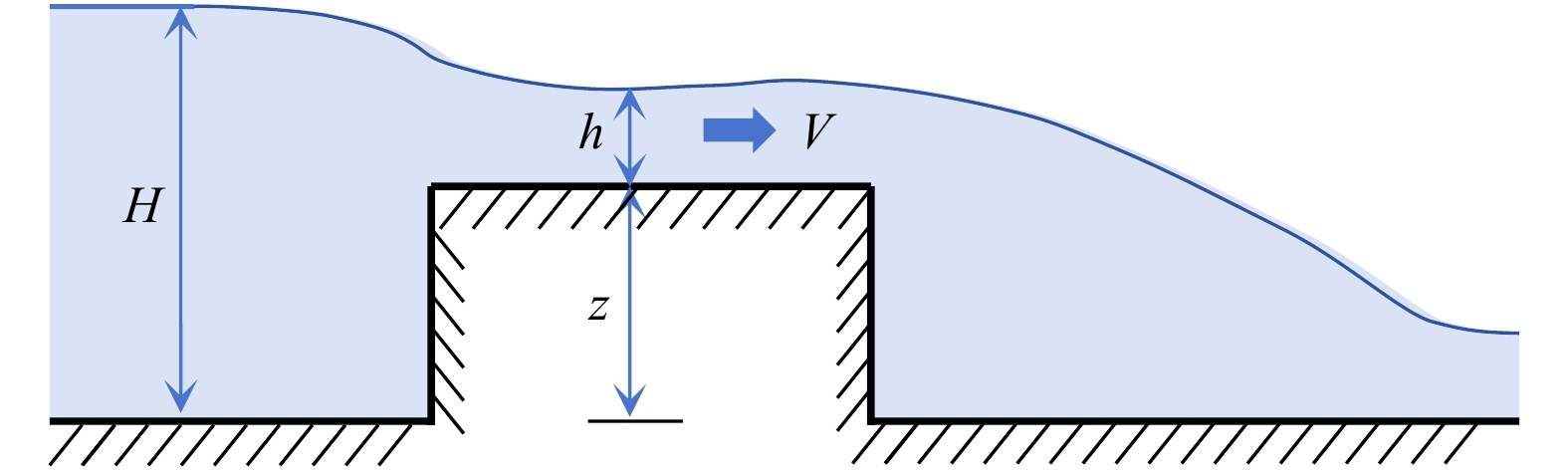
图 5 湿床河道溃坝波示意图[38]
1~4. 溃坝波段编号;M,N,R. 溃坝波段交界位置;O为原点位置;t0. 激波与稀疏波的时间差;u. 2段处流速;ξ. 激波的波前速度;ξt. t时刻激波速度;ht. 2段处水深;hc. 3段处水深;h1. 下游段水深;uc. 3段处流速;xM. 1段和2段交界位置M处坐标;xN. 2段和3段交界位置N处坐标;xR. 3段和4段交界位置R处坐标;下同
Figure 5. Schematic diagram of dam-break wave in a wet-bed channel
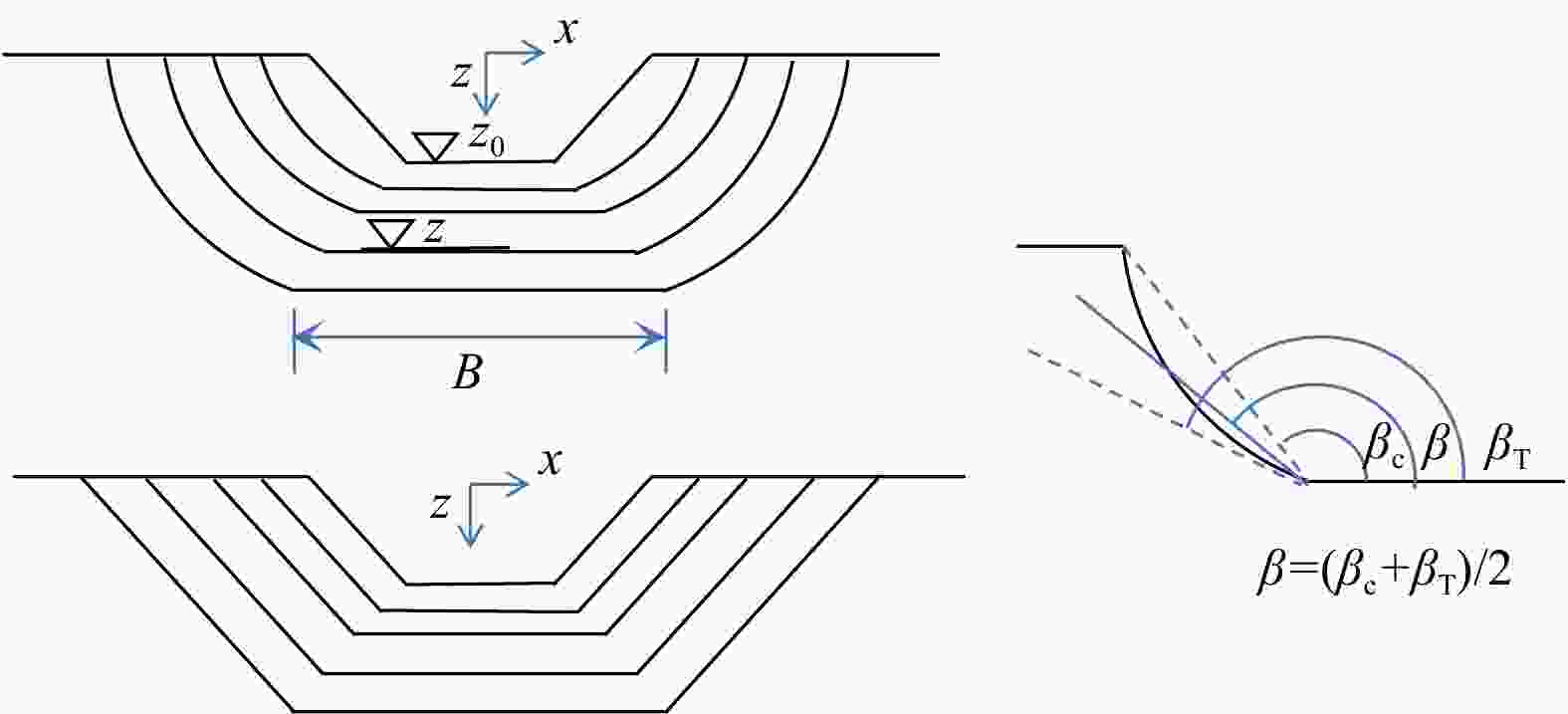
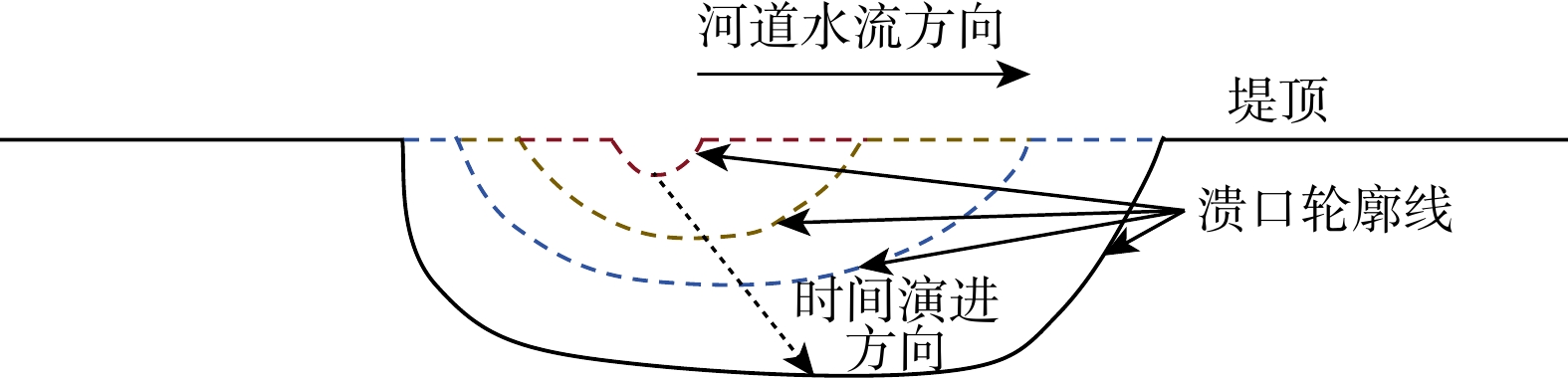
图 8 溃口横向扩展示意图[109]
z0. 溃口底部初始高度;β为梯形斜面与水平面的夹角;βc. 割线夹角;βr. 切线夹角
Figure 8. Schematic diagram of lateral breach expansion
表 1 3个现场溃决试验对比
Table 1. Comparison of three field dam breach experiments
现场试验名称 堤坝材料类型 坝高/m 相关计算模型 欧洲IMPACT
计划项目黏性土、非黏性
土、卵砾石4.5~6 HR BREACH、NWS
BREACH、DEICH、
SIMBA、Sobek、Firebird美国农业部
试验粉砂、黏性土 1.3~2.3 SIMBA、WINDAM 南京水利科学
研究院试验黏性土 9.7 DB-NHRI 表 2 国内外常见峰值流量参数模型汇总
Table 2. Summary of commonly used peak discharge parameter models worldwide
参数模型 峰值流量表达式 案例量 参数量 KIRKPATRICK[39] $ {Q}_{\text{p}}=1.268{({{h}_{\text{w}}}+0.3)}^{2.5} $ 19 1 Soil Conservation Seerive[41] $ {Q}_{\text{p}}=16.6{({{h}_{\text{w}}})}^{1.85} $ 13 1 HAGEN[42] $ {Q}_{\text{p}}=0.54{({{h}_{\text{d}}}S)}^{0.5} $ 6 2 SINGH等[43] $ {Q}_{\text{p}}=13.4{({{h}_{\text{d}}})}^{1.89},{Q}_{\text{p}}=1.776{({{V}_{\text{w}}})}^{0.47} $ 28 1 MACDONALD等[44] $ {Q}_{\text{p}}=1.154{({{V}_{\text{w}}}{{h}_{\text{w}}})}^{0.412} $ 23 2 COSTA[45] $ {Q}_{\text{p}}=0.981{({{h}_{\text{d}}}{{V}_{\text{w}}})}^{0.42} $ 31 2 EVANS[46] $ {Q}_{\text{p}}=0.72{({{V}_{\text{w}}})}^{0.53} $ 29 1 U. S. Bureau of Reclamation[47] $ {Q}_{\text{p}}=19.1{({{h}_{\text{w}}})}^{1.85} $ 21 1 FROCHLICH[48] $ {Q}_{\text{p}}=0.607{({{V}_{\text{w}}})}^{0.295}{({{h}_{\text{w}}})}^{1.24} $ 22 2 WALDER等[49] $ {Q}_{\text{p}}=0.031{(g)}^{0.5}{({{V}_{\text{w}}})}^{0.47}{({{h}_{\text{w}}})}^{0.15}{({{h}_{\text{b}}})}^{0.94} $ 18 3 XU等[50] $ {Q}_{\text{p}}=0.175{g}^{0.5}V_{\text{w}}^{5/6}{({{h}_{\text{d}}}/{{h}_{\text{r}}})}^{0.199}{({V_{\text{w}}^{1/3}}/{{h}_{\text{w}}})}^{-1.274}{{\mathrm{e}}}^{{{B}_{4}}} $ 75 3 PIERCE等[51] $ {Q}_{\text{p}}=0.017\;6{({{V}_{\text{w}}}{{h}_{\text{w}}})}^{0.606},{Q}_{\text{p}}=0.038{({{V}_{\text{w}}})}^{0.475}{({{h}_{\text{w}}})}^{1.09} $ 87 2 THORNTON等[52] $ {Q}_{\text{p}}=0.120\;2{L}^{1.785\;6}\text{,}{Q}_{\text{p}}=0.863{V}^{0.335}h_{\text{d}}^{1.833}W_{\text{ave}}^{-0.663}\text{,}{Q}_{\text{p}}=0.012{V}^{0.493}h_{\text{d}}^{1.205}L_{}^{0.226} $ 38 3 PENG等[53] $ \dfrac{{Q}_{\text{p}}}{{g}^{0.5}h_{\text{d}}^{2.5}}={\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{-1.417}{\left(\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}\right)}^{-0.265}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{-0.471}{\left(\dfrac{V_{\text{l}}^{1/3}}{{h}_{\text{d}}}\right)}^{1.569}{{\mathrm{e}}}^{\alpha } $ 45 4 DE LOORENZO等[54] $ \begin{aligned}{Q}_{\text{p}}&=0.321{g}^{0.258}(0.07{V_{\text{w}}^{}})^{0.485}h_{\text{b}}^{0.802}(漫顶)\\{Q}_{\text{p}}&=0.347{g}^{0.263}(0.07{V_{\text{w}}^{}})^{0.474}h_{\text{b}}^{-2.151}h_{\text{w}}^{2.992}(渗透破坏)\end{aligned} $ 14 3 HOOSHYARIPOR等[55] $ {Q}_{\text{p}}=0.021\;2{({{V}_{\text{w}}})}^{0.542\;9}{({{h}_{\text{w}}})}^{0.871\;3},{Q}_{\text{p}}=0.045\;4{({{V}_{\text{w}}})}^{0.448}{({{h}_{\text{w}}})}^{1.156} $ 93 2 AZIMI等[56] $ {Q}_{\text{p}}=0.016\;6{(gS)}^{0.5}h $ 70 2 FROEHLICH[40] $ {Q}_{\text{p}}=0.017\;5{k}_{\text{M}}{k}_{\text{H}}{\text{(}g{{V}_{\text{w}}}{{h}_{\text{w}}}{h_{\text{b}}^{\text{2}}}/{{W}_{\text{ave}}}\text{)}}^{0.5} $ 41 4 黄委会科研所[57] $ {Q}_{\text{p}}=0.296(\sqrt{g}){({B_{\mathrm{R}}}/{B})}^{0.4}{B}{H}^{1.5} $ − 3 戴荣尧等[58] $ {Q}_{\text{p}}=0.27(\sqrt{g}){({{L}_{0}}/{B_{\mathrm{R}}})}^{1/10}{({B_{\mathrm{R}}}/B)}^{1/3}B{(H-K{\textit{z}})}^{1.5} $ − 3 国家防汛抗旱总指挥部等[59] $ \begin{aligned}{Q}_{\text{b}}&={c}_{1}\sigma B\sqrt{2g}h_{\text{w}}^{\text{1.5}}(堤防溃口出流)\\{Q}_{\text{b}}&={c}_{\text{v}}{k}_{\text{s}}{c}_{\text{d}}\sqrt{2\mathrm{g}}\left[\dfrac{2}{3}{b}_{\text{s}}{(H-{\textit{z}})}^{1.5}+\dfrac{8}{15m}{(H-{\textit{z}})}^{2.5}\right](土石坝漫顶溃决)\end{aligned} $ − 2 邓刚等[60] $ {Q}_{\text{p}}={B}_{\text{b}}{c}_{\text{d}}\sqrt{2g}{(H-{\textit{z}})}^{3/2}+\dfrac{4{c}_{\text{d}}m\sqrt{2g}}{5}\left\{{(H-{\textit{z}})}^{5/2}[1-{(1-k)}^{5/2}]\right\} $ − 2 石振明等[61] $ {Q}_{\text{p}}=3.130h_{\text{d}}^{0.120}W_{\text{d}}^{0.302}V_{\text{d}}^{\text{-0.106}}V_{\text{l}}^{\text{0.453}}{{\mathrm{e}}}^{\alpha } $ 26 4 梅世昂等[62] $ \dfrac{{Q}_{\text{p}}}{{V}_{\text{w}}{g}^{0.5}h_{\text{w}}^{-0.5}}=\begin{cases} {\left(\dfrac{V_{\text{w}}^{1/3}}{{h}_{\text{w}}}\right)}^{-1.58}{\left(\dfrac{{h}_{\text{w}}}{{h}_{\text{b}}}\right)}^{-0.76}{\left(\dfrac{{h}_{\text{d}}}{{h}_{\text{r}}}\right)}^{0.10}{\mathrm{e}}^{-4.55}(均质坝)\\{\left(\dfrac{V_{\text{w}}^{1/3}}{{h}_{\text{w}}}\right)}^{-1.51}{\left(\dfrac{{h}_{\text{w}}}{{h}_{\text{b}}}\right)}^{-1.09}{\left(\dfrac{{h}_{\text{d}}}{{h}_{\text{r}}}\right)}^{-0.12}{\mathrm{e}}^{-3.61}(心墙坝)\end{cases} $ 154 3 齐子杰等[63] $ \dfrac{{Q}_{\text{p}}}{{g}^{0.5}h_{\text{d}}^{2.5}}=0.828{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{-0.128}{\left(\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}\right)}^{-0.432}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{-0.394}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{1.151} $ 65 4 单熠博等[64] $ {Q}_{\text{p}}={\left({h}_{\text{d}}\right)}^{-0.229}{\left({W}_{\text{d}}\right)}^{-0.04}{\left({V}_{\text{l}}\right)}^{0.558}{\mathrm{e}}^{{{C}_{\text{m}}}} $ 44 3 FROEHLICH[65] $ {Q}_{\text{p}}={K}_{Q}{\left(\dfrac{V_{\text{l}}^{1/3}}{{h}_{\text{d}}}\right)}^{2}\sqrt{gh_{\text{d}}^{5}} $ 42 2 焦煦等[66] $ \begin{aligned}{Q}_{\text{p}}&=10.03h_{\text{d}}^{2.816}V_{\text{l}}^{\text{1.557}}h_{\text{b}}^{\text{-3.661}}({h}_{\text{d}} > 70),\;{Q}_{\text{p}}=h_{\text{d}}^{\text{1.629}}V_{\text{l}}^{\text{0.826}}h_{\text{b}}^{\text{-0.053}}(30\leq {h}_{\text{d}}\leq 70)\\{Q}_{\text{p}}&=194.7h_{\text{d}}^{1.163}V_{\text{l}}^{\text{-0.084}}h_{\text{b}}^{-0.636}({h}_{\text{d}} < 30)\end{aligned} $ 75 3 GUAN等[67] $ {Q}_{\text{p}}=910h_{\text{d}}^{-0.25}V_{\text{l}}^{0.56}{{\mathrm{e}}}^{{{\alpha }_{2}}} $ 46 2 冯震宇等[68] $ {Q}_{\text{p}}=0.043{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{1.717}{\left(\dfrac{{W}_{\text{d}}}{{h}_{\text{d}}}\right)}^{1.725}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{-2.03}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{1.865}{{\mathrm{e}}}^{{{\alpha }_{1}}}{{\mathrm{e}}}^{{{\beta }_{1}}} $ 48 4 注:Qp为峰值流量;Qb为溃口实时流量;hw为溃口底部以上水深;S为库容;Vw为溃口底部以上水库库容;hr为参考坝高15 m;L为坝体长度;Wave为坝体平均宽度;Hr为参考坝高1 m;Wd为坝体宽度;Vd为坝体体积;Vl为溃坝时库容;L0为库长;BR为库宽;B为溃口平均宽度;H为坝前水深;z为坝体残留高度;K为系数,详见文献[58];B4为考虑坝型、溃决类型与坝高的拟合指数,见文献[50];kM、kH为系数,具体见文献[40];c1为自由溢流流量系数,σ为淹没系数,cv为行进流速改正系数,cd为流量系数,ks为流量修正系数,bs为溃口实时底宽,具体见文献[59];Bb为溃口最终底宽;k为水头跌落系数,见文献[60];α为侵蚀度,见文献[61];Cm为考虑颗粒组成的冲蚀因子,具体见文献[64];KQ为坝体可蚀系数,具体取值见文献[65];α2为可蚀系数,具体取值见文献[67];α1为坝体材料系数,β1为坝体诱因系数,具体取值见文献[68];下同 表 3 国内外常见溃口平均宽度参数模型汇总
Table 3. Summary of commonly used average breach width parameter models worldwide
参数模型 溃口宽度表达式 案例量 参数量 U. S. Bureau of Reclamation[47] $ {B}_{\text{ave}}=3{h}_{\text{w}} $ 63 1 VONTHUN等[69] $ {B}_{\text{ave}}=2.5{h}_{\text{w}}+{C}_{\text{b}} $ 63 1 FROCHLICH[48] $ {B}_{\text{ave}}=0.180\;3{K}_{0}{({{V}_{\text{w}}})}^{0.32}{({{h}_{\text{b}}})}^{0.19} $ 63 2 XU等[50] $ \dfrac{{B}_{\text{ave}}}{{h}_{\text{b}}}=0.787{\left(\dfrac{{h}_{\text{d}}}{{h}_{\text{r}}}\right)}^{0.133}{\left(\dfrac{V_{\text{w}}^{1/3}}{{h}_{\text{w}}}\right)}^{0.652}{\mathrm{e}}^{{{B}_{3}}} $ 47 2 PENG等[53] $ \begin{aligned}\dfrac{{B}_{\text{f}}}{{H}_{\text{r}}}&={\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{0.752}{\left(\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}\right)}^{0.315}{\left(\dfrac{V_{\text{d}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{-0.243}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{0.682}{\mathrm{e}}^{\alpha }(溃口顶宽)\\\dfrac{{B}_{\text{b}}}{{h}_{\text{d}}}&=0.004\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)+0.050\left(\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}\right)-0.044\left(\dfrac{V_{\text{d}}^{\text{1/3}}}{{h}_{\text{d}}}\right)+0.088\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)+\alpha (溃口底宽)\end{aligned} $ 10 4 FROEHLICH[40] $ {B}_{\text{ave}}=0.27{k}_{\text{M}}{({{V}_{\text{w}}})}^{1/3} $ 63 1 黄委会科研所[57] $ {B}_{\text{ave}}=k{S}^{0.25}{B_{\mathrm{R}}}^{0.25}{H}^{0.5} $ - 3 戴荣尧等[58] $ {B}_{\text{ave}}=k{S}^{0.25}{B_{\mathrm{R}}}^{1/7}{H}^{0.5} $ - 3 国家防汛抗旱总指挥部等[59] $ \begin{aligned}{B}_{\text{ave}}&=4.5({{\lg }}{{B}_{\text{r}}})^{3.5}+50(汇流点)\\{B}_{\text{ave}}&=1.9({{\lg }}{{B}_{\text{r}}})^{4.8}+20(其他)\end{aligned} $ - 1 刘建康等[70] $ {B}_{\text{ave}}=0.367{\left(\dfrac{S}{{V}_{\text{s}}}\right)}^{0.195}{\left(\dfrac{{B}_{\text{e}}}{\tan \varphi }\right)}^{0.337}{H}^{0.5} $ 31 3 石振明等[61] $ \begin{aligned}{B}_{\text{f}}&=1.593{h}_{\text{d}}+85.249\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}-3.438\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}+15.963\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}+\alpha (溃口顶宽)\\{B}_{\text{b}}&=-0.006h_{\text{d}}^{\text{2}}-0.047\dfrac{h_{\text{d}}^{\text{2}}}{{W}_{\text{d}}}+0.017V_{\text{d}}^{\text{1/3}}+0.047V_{\text{l}}^{\text{1/3}}+\alpha {h}_{\text{d}}(溃口底宽)\end{aligned} $ 16 4 梅世昂等[62] $ \dfrac{{B}_{\text{ave}}}{{h}_{\text{b}}}=\begin{cases} {\left(\dfrac{V_{\text{w}}^{1/3}}{{h}_{\text{w}}}\right)}^{0.84}{\left(\dfrac{{h}_{\text{w}}}{{h}_{\text{b}}}\right)}^{2.30}{\left(\dfrac{{h}_{\text{d}}}{{h}_{\text{r}}}\right)}^{0.06}{\mathrm{e}}^{-0.90}(均质坝)\\{\left(\dfrac{V_{\text{w}}^{1/3}}{{h}_{\text{w}}}\right)}^{0.55}{\left(\dfrac{{h}_{\text{w}}}{{h}_{\text{b}}}\right)}^{1.97}{\left(\dfrac{{h}_{\text{d}}}{{h}_{\text{r}}}\right)}^{-0.07}{\mathrm{e}}^{-0.09}(心墙坝)\end{cases} $ 63 3 齐子杰[63] $ \begin{aligned}\dfrac{{B}_{\text{f}}}{{H}_{\text{r}}}&=1.162{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{1.016}{\left(\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}\right)}^{0.429}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{0.444}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{0.381}(溃口顶宽)\\\dfrac{{B}_{\text{b}}}{{H}_{\text{r}}}&=-12.55+0.208\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}+17.38\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}-1.941\dfrac{V_{\text{d}}^{\text{1/3}}}{{h}_{\text{d}}}+7.371\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}(溃口底宽)\end{aligned} $ 12 4 冯震宇等[68] $ \begin{aligned}{B}_{\text{f}}&=0.462{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{1.77}{\left(\dfrac{{W}_{\text{d}}}{{h}_{\text{d}}}\right)}^{0.081}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{1.419}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{-0.457}{\mathrm{e}}^{{{\alpha }_{1}}}{\mathrm{e}}^{{{\beta }_{1}}}(溃口顶宽)\\{B}_{\text{b}}&=7.83\times {10}^{-9}{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{6.634}{\left(\dfrac{{W}_{\text{d}}}{{h}_{\text{d}}}\right)}^{1.874}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{-1.07}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{-1.027}{\mathrm{e}}^{{{\alpha }_{1}}}{\mathrm{e}}^{{{\beta }_{1}}}(溃口底宽)\end{aligned} $ 11 4 注:Bf为溃口最终顶宽;Br为河道宽度;Vs为坝体单宽体积;Be为有效坝长;φ为内摩擦角;Cb为经验拟合系数,取值见文献[69];B3为系数,详见文献[32];k为系数,见文献[57];对于漫顶溃坝,K0=1.4,对于渗透破坏溃坝,K0=1.0;对于漫顶溃坝,kM=1.3,对于渗透破坏溃坝,kM=1.0;下同 表 4 国内外常见溃决历时参数模型汇总
Table 4. Summary of commonly used breach duration parameter models worldwide
参数模型 溃坝历时表达式 案例量 参数量 MACDONALD等[44] $ {T}_{\text{f}}=0.017\;9{(0.026\;1{{({{V}_{\text{w}}}{{h}_{\text{w}}})}^{0.769}})}^{0.364} $ 39 2 U.S. Bureau of Reclamation[47] $ {T}_{\text{f}}=0.011{B}_{\text{ave}} $ 39 1 FROCHLICH[48] $ {T}_{\text{f}}=0.002\;54{({{V}_{\text{w}}})}^{0.53}{({{h}_{\text{b}}})}^{-0.9} $ 39 2 XU等[50] $ \dfrac{{T}_{\text{f}}}{{T}_{\text{r}}}=0.304{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{0.707}{\left(\dfrac{V_{\text{w}}^{\text{1/3}}}{{h}_{\text{w}}}\right)}^{1.228}{\mathrm{e}}^{{{B}_{5}}} $ 34 2 国家防汛抗旱总指挥部等[59] $ {T}_{\text{f}}=1.527({B}_{\text{ave}}-10) $ − 1 FROEHLICH[40] $ {T}_{\text{f}}=63.2{({{V}_{\text{w}}}/(g{{h}_{\text{b}}}{{}^{2}}))}^{0.5}/3\;600 $ 39 2 PENG等[53] $ \dfrac{{T}_{\text{f}}}{{T}_{\text{r}}}={\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{0.262}{\left(\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}\right)}^{-0.024}{\left(\dfrac{V_{\text{d}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{-0.103}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{0.705}{\mathrm{e}}^{{{a}_{9}}} $ 14 4 石振明等[61] $ {T}_{\text{f}}=h_{\text{d}}^{0.275}W_{\text{d}}^{-1.224}V_{\text{d}}^{\text{0.439}}V_{\text{l}}^{\text{0.232}}{\mathrm{e}}^{\alpha } $ 12 4 梅世昂等[62] $ \dfrac{{T}_{\text{f}}}{{T}_{0}}=\begin{cases} {\left(\dfrac{V_{\text{w}}^{1/3}}{{h}_{\text{w}}}\right)}^{0.56}{\left(\dfrac{{h}_{\text{w}}}{{h}_{\text{b}}}\right)}^{-0.85}{\left(\dfrac{{h}_{\text{d}}}{{h}_{\text{r}}}\right)}^{-0.32}{\mathrm{e}}^{-0.20}(均质坝)\\{\left(\dfrac{V_{\text{w}}^{1/3}}{{h}_{\text{w}}}\right)}^{1.52}{\left(\dfrac{{h}_{\text{w}}}{{h}_{\text{b}}}\right)}^{-11.36}{\left(\dfrac{{h}_{\text{d}}}{{h}_{\text{r}}}\right)}^{-0.43}{\mathrm{e}}^{-1.57}(心墙坝)\end{cases} $ 39 3 齐子杰等[63] $ \dfrac{{T}_{\text{f}}}{{T}_{\text{r}}}=0.05{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{1.237}{\left(\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}\right)}^{-1.371}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{-0.905}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{0.736} $ 16 4 冯震宇等[68] $ {T}_{\text{f}}=2.352{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{1.4324}{\left(\dfrac{{W}_{\text{d}}}{{h}_{\text{d}}}\right)}^{-0.58}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{0.623}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{1.625}{\mathrm{e}}^{{{\alpha }_{1}}}{\mathrm{e}}^{{{\beta }_{1}}} $ 18 4 注:$T_{\mathrm{f}} $为溃决历时;$T_{\mathrm{r}} $为单位时间1 h;$a_9 $为经验拟合系数,见参考文献[53];B5为系数,见文献[50];下同 表 5 国内外常见溃口深度参数模型汇总
Table 5. Summary of commonly used breach depth parameter models worldwide
参数模型 溃口深度表达式 案例量 参数量 PENG等[53] $ \dfrac{{h}_{\text{b}}}{{H}_{\text{r}}}={\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{0.882}{\left(\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}\right)}^{-0.041}{\left(\dfrac{V_{\text{d}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{-0.099}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{0.139}{\mathrm{e}}^{\alpha } $ 21 4 石振明等[61] $ {h}_{\text{b}}=h_{\text{d}}^{0.840}W_{\text{d}}^{-0.169}V_{\text{d}}^{0.089}V_{\text{l}}^{\text{0.040}}{\mathrm{e}}^{\alpha } $ 26 4 齐子杰等[63] $ \dfrac{{h}_{\text{b}}}{{H}_{\text{r}}}=2.266+0.403\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}-14.668\dfrac{{h}_{\text{d}}}{{W}_{\text{d}}}-0.409\dfrac{V_{\text{d}}^{\text{1/3}}}{{h}_{\text{d}}}+1.181\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}} $ 10 4 焦煦等[66] $ {h}_{\text{b}}=\alpha (1.636h_{\text{d}}^{0.791}+0.003V_{\text{l}}^{\text{1.183}}) $ 23 2 冯震宇等[68] $ {h}_{\text{b}}=0.102{\left(\dfrac{{h}_{\text{d}}}{{H}_{\text{r}}}\right)}^{0.68}{\left(\dfrac{{W}_{\text{d}}}{{h}_{\text{d}}}\right)}^{0.299}{\left(\dfrac{V_{\text{d}}^{1/3}}{{h}_{\text{d}}}\right)}^{-0.434}{\left(\dfrac{V_{\text{l}}^{\text{1/3}}}{{h}_{\text{d}}}\right)}^{0.174}{\mathrm{e}}^{{{\alpha }_{1}}}{\mathrm{e}}^{{{\beta }_{1}}} $ 19 4 表 6 国内外常见一维计算模型汇总
Table 6. Summary of commonly used one-dimensional computational models worldwide
来源 溃口形状 冲蚀计算公式 流量计算公式 备 注 CRISTOFANO[75] 恒定底宽的梯形 — 宽顶堰公式 不考虑溃口的横向冲蚀,时间步内只考虑溃口的竖向冲蚀量 H-W[76] 抛物线形 Schoklitsch推移质公式 宽顶堰公式 溃口形状为抛物线,溃口顶宽为溃口深度3.5倍;溃口坡度为坝体材料的内摩擦角并保持不变 BRDAM[77] 抛物线形 Schoklitsch推移质公式 宽顶堰公式 在Harris-Wagner模型基础上改进,溃口侧壁坡度恒定为45° LOU[78] 根据剪应力求解 Duboy推移质模型&Einstein悬移质公式 Saint-Venant方程 根据剪应力来分析溃口的形状 P-T[79] 根据水流速度计算溃口顶宽 Meyer-Peter&Muller推移质公式 Saint-Venant方程 根据河床稳定理论确定溃口宽度和水流速度的关系,流量达到峰值后溃口宽度不再变化 DAMBRK[74] 由溃口底宽、高度和侧壁坡度决定 经验公式 宽顶堰公式 根据Froelich冲蚀关系经验方程计算溃口侵蚀过程 NOGUEIRA[80] 断面水深为与溃口纵断面距离的余弦函数 Meyer-Peter & Muller推移质公式 Saint-Venant方程 在Lou模型的基础上进行改进,考虑了溃口侧壁滑塌对溃口扩展的影响 BEED[81] 由溃口底宽、高度和侧壁坡度决定 Einstein – Brown推移质公式 宽顶堰公式 根据楔形体稳定分析方法确定溃口侧壁形状,考虑渗透力、扬压力分析楔形体稳定性 BREACH[82] 矩形和梯形 Smart改进的Meyer-Peter & Muller推移质公式 宽顶堰公式 溃口稳定性根据材料性质判断,同时考虑了水压力过大造成的溃口坍塌影响 NCP BREACH[89] 抛物线形 经验公式 经验公式 根据室内试验数据得到溃口流量参数、溃口形状和冲蚀计算公式参数 ED BREACH[90] 梯形 Meyer-Peter & Muller推移质公式 宽顶堰公式 对BREACH模型的改进模型 BRES[91] 梯形 Bagnold-Visser、Engelund-Hansen和Van Rijn公式 宽顶堰公式 分为5个阶段研究溃坝过程,各阶段分别采用不同的冲蚀公式进行计算 HR BREACH[92] Mohammed法 Yang公式、Visser公式和Chen-Anderson 公式 宽顶堰公式 在BRES模型冲蚀计算方法的基础上,引入有效剪应力计算溃口形状 SIMBA[93] 矩形或梯形 引入坝料冲蚀系数模拟坝体冲蚀 宽顶堰公式 模拟陡坎侵蚀,将溃口过程分为4个阶段,采用基于能量法或剪应力法的陡坎移动公式模拟溯源冲刷 WINDAM[94] 矩形或梯形 引入坝料冲蚀系数模拟坝体冲蚀 宽顶堰公式 在SIMBA模型的基础上,考虑了坡面植被的影响 陈生水等[95]
DB-NHRI矩形或梯形 修正的Meyer-Peter & Muller 推移质公式 宽顶堰公式 采用溃口边坡稳定性分析来计算边坡楔形体的稳定性,从而判断溃口扩展,通过下游坝体冲槽和坝顶溃口流量平衡建立二者发展过程的相互影响 傅旭东等[96] 梯形 泥沙输移公式 Saint-Venant方程 基于Exner方程,考虑床沙活动层和泥沙的侧向补给,得到河床变形高度,考虑并采用Osman和Thorne[97]提出的河堤稳定性分析方法 CHANG等[98] 梯形 经验公式 宽顶堰公式 冲蚀速率经验公式由原位试验得到,并在计算过程中考虑了溃口深度对冲蚀的影响 DHI Water Environment[99]
MIKE11DB梯形 Engelund-Hansen推移质公式,也可自定义冲蚀系 宽顶堰公式 可采用两种冲蚀计算防范,自定义输入参数,作为溃坝计算边界条件 WU[100] 矩形、梯形 直线型公式 宽顶堰公式 使用Osman和Thorne提出的河堤稳定性分析方法,并考虑了溯源冲刷过程 CHEN等[88]
DB-IWHR圆弧形 经验双曲线型公式 宽顶堰公式 以流速为步长进行计算,在溃口深度采用冲蚀计算的基础上,溃口横向扩展采用土坡稳定分析中的圆弧滑动法进行 BRUNNER[101]
HEC-RAS多边形 泥沙输移公式 Saint-Venant方程 溃决过程采用BREACH模型,洪水下游演进,采用四点隐式有限差分格式对非线性方程进行离散求解 ZHAO[102] 梯形 基于力矩平衡的侵蚀率公式 宽顶堰公式 将溃口发展过程分为表面侵蚀、切头侵蚀、横向侵蚀3个阶段,切头侵蚀与横向侵蚀过程以黏土块的形式进行 沈鸿杰等[103]
改进DB-IWHR梯形 经验双曲线型公式 宽顶堰公式 采用修正的Shields曲线改进DB-IWHR模型中临界剪应力的计算 巨江等[104]
DB-D梯形 溃口下切扩散方程 宽顶堰公式 采用溃坝冲刷过程扩散模型,并给出溃口纵剖面侵蚀下切与横断面展宽的解析解及冲刷系数计算公式 吕佳豪等[105] 梯形条分 — Saint-Venant方程 基于Godunov有限体积格式的一维溃坝洪水演进模型,采用条分法处理复杂河道断面 -
[1] 中华人民共和国水利部. 第一次全国水利普查公报[M]. 北京: 中国水利水电出版社, 2013.Ministry of Water Resources of the People's Republic of China. Bulletin of first national census for water[M]. Beijing: China Water & Power Press, 2013. (in Chinese) [2] 中华人民共和国水利部. 2021年全国水利发展统计公报[M]. 北京: 中国水利水电出版社, 2022.Ministry of Water Resources of the People's Republic of China. 2021 Statistic bulletin on China water activities[M]. Beijing: China Water & Power Press, 2022. (in Chinese) [3] 水利部大坝安全管理中心. 全国水库垮坝登记册[R]. 南京: 水利部大坝安全管理中心, 2018.Dam Safety Management Center of the Ministry of Water Resources. National reservoir dam collapse register[R]. Nanjing: Dam Safety Management Center of the Ministry of Water Resources, 2018. (in Chinese) [4] 汝乃华, 牛运光. 大坝事故与安全-土石坝[M]. 北京: 中国水利水电出版社, 2001.RU N H, NIU Y G. Embankment dam incidents and safety of large dams[M]. Beijing: China Water & Power Press, 2001. (in Chinese) [5] 李君纯. 沟后面板坝溃决的研究[J]. 水利水运科学研究, 1995(4): 425-434. doi: 10.16198/j.cnki.1009-640x.1995.04.011LI J C. A research for break of Gouhou face dam[J]. Hydro-Science and Engineering, 1995(4): 425-434. (in Chinese with English abstract doi: 10.16198/j.cnki.1009-640x.1995.04.011 [6] 陈生水. 土石坝溃决机理与溃坝过程模拟[M]. 北京: 中国水利水电出版社, 2012.CHEN S S. Failure mechanism and simulation of earth-rock dam failure process[M]. Beijing: China Water & Power Press, 2012. (in Chinese) [7] 陈生水, 钟启明. 土石坝溃坝数学模型及应用[M]. 北京: 中国水利水电出版社, 2019.CHEN S S, ZHONG Q M. Numerical models for earth-rock dam breaching and their applications[M]. Beijing: China Water & Power Press, 2019. (in Chinese) [8] 赵悬涛, 刘昌军, 王文川, 等. 射月沟水库溃坝洪水模拟及溃坝原因分析[J]. 中国农村水利水电, 2022(5): 171-177.ZHAO X T, LIU C J, WANG W C, et al. Dam break flood simulation of Sheyuegou reservoir and reasons for the dam break[J]. China Rural Water and Hydropower, 2022(5): 171-177. (in Chinese with English abstract [9] GALLEGOS H A, SCHUBERT J E, SANDERS B F. Two-dimensional, high-resolution modeling of urban dam-break flooding: A case study of Baldwin Hills, California[J]. Advances in Water Resources, 2009, 32(8): 1323-1335. [10] LAND L F. Mathematical simulations of the Toccoa Falls, Georgia, dam-break flood[J]. JAWRA Journal of the American Water Resources Association, 1980, 16(6): 1041-1048. [11] PIRULLI M, BARBERO M, MARCHELLI M, et al. The failure of the Stava Valley tailings dams (northern Italy): Numerical analysis of the flow dynamics and rheological properties[J]. Geoenvironmental Disasters, 2017, 4(1): 3. [12] DEVKOTA L, GIRI S, CROSATO A, et al. Impact of the Koshi barrage and embankments on river morphology and dynamics[C]//Anon. Seventh International Conference on Water Resource and Renewable Energy Development in Asia. [S. l. ]: [s. l. ], 2018: 3-15. [13] AURELI F, MARANZONI A, PETACCIA G. Review of historical dam-break events and laboratory tests on real topography for the validation of numerical models[J]. Water, 2021, 13(14): 1968. doi: 10.3390/w13141968 [14] SILVA ROTTA L H, ALCÂNTARA E, PARK E, et al. The 2019 Brumadinho tailings dam collapse: Possible cause and impacts of the worst human and environmental disaster in Brazil[J]. International Journal of Applied Earth Observation and Geoinformation, 2020, 90: 102119. doi: 10.1016/j.jag.2020.102119 [15] ZIN W W, KAWASAKI A, TAKEUCHI W, et al. Flood hazard assessment of Bago River basin, Myanmar[J]. Journal of Disaster Research, 2018, 13(1): 14-21. [16] ANNUNZIATO A, SANTINI M, PROIETTI C, et al. Modelling and validation of the Derna dam break event[J]. GeoHazards, 2024, 5(2): 504-529. doi: 10.20944/preprints202403.1298.v1 [17] 胡大儒, 吴述彧, 罗超鹏, 等. 澜沧江某巨型堆积体蓄水失稳诱发涌浪预测[J]. 地质科技通报, 2024, 43(6): 78-88. doi: 10.19509/j.cnki.dzkq.tb20230598HU D R, WU S Y, LUO C P, et al. Prediction of the wave induced by a gaint accumulation impoundment instability in Lantsang River[J]. Bulletin of Geological Science and Technology, 2024, 43(6): 78-88. (in Chinese with English abstract doi: 10.19509/j.cnki.dzkq.tb20230598 [18] 吴昌瑜, 丁金华. 九江长江干堤溃口段破坏机理及处理措施[J]. 岩土工程学报, 2001, 23(5): 557-562.WU C Y, DING J H. Failure mechanism and treatment of a burst stretch of the Yangtze River dike in Jiujiang[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 557-562. [19] 杜勇江, 王运生, 邹子南, 等. 动水冲刷作用下堆积体岸坡的渐进破坏过程分析[J]. 地质科技通报, 2024, 43(6): 226-234. doi: 10.19509/j.cnki.dzkq.tb20240213DU Y J, WANG Y S, ZOU Z N, et al. Progressive analysis of the progressive failure process of accumulated bank slope under dynamic water scour[J]. Bulletin of Geological Science and Technology, 2024, 43(6): 226-234. (in Chinese with English abstract doi: 10.19509/j.cnki.dzkq.tb20240213 [20] 陈启刚, 张大伟, 王忠祥, 等. 堤防溃口水流特性与封堵技术研究进展[J]. 中国防汛抗旱, 2021, 31(8): 1-6. doi: 10.16867/j.issn.1673-9264.2021186CHEN Q G, ZHANG D W, WANG Z X, et al. Progress in flow characteristics and closure technology of dike breaches[J]. China Flood & Drought Management, 2021, 31(8): 1-6. (in Chinese with English abstract doi: 10.16867/j.issn.1673-9264.2021186 [21] 王忠祥, 张大伟. 堤防漫顶溃决物理模型试验研究进展[J]. 中国水利水电科学研究院学报(中英文), 2024, 22(1): 36-48. doi: 10.13244/j.cnki.jiwhr.20230118WANG Z X, ZHANG D W. Progress in physical modeling experiments of dike overtopping breach[J]. Journal of China Institute of Water Resources and Hydropower Research, 2024, 22(1): 36-48. (in Chinese with English abstract doi: 10.13244/j.cnki.jiwhr.20230118 [22] 果鹏, 夏军强, 周美蓉, 等. 生产堤溃口展宽过程的概化模型试验研究[J]. 水科学进展, 2020, 31(2): 249-259. doi: 10.14042/j.cnki.32.1309.2020.02.011GUO P, XIA J Q, ZHOU M R, et al. Investigation into lateral widening process of farm dike breach using a sketched physical model[J]. Advances in Water Science, 2020, 31(2): 249-259. (in Chinese with English abstract doi: 10.14042/j.cnki.32.1309.2020.02.011 [23] MORRIS M, HASSAN M. IMPACT: Investigation of extreme flood processes and uncertainty: A European research project[C]//Anon. Proceedings of the 40th DEFRA Flood and Coastal Management Conference. [S. l. ]: [s. l. ], 2005. [24] BRITTON S L, HANSON G J, COOK K R, et al. Breach widening observations from earthen embankment tests[C]//Anon. American Society of Agricultural and Biological Engineers. [S. l. ]: [s. l. ], 2004. [25] HANSON G J, HUNT S L. Lessons learned using laboratory JET method to measure soil erodibility of compacted soils[J]. Applied Engineering in Agriculture, 2007, 23(3): 305-312. doi: 10.13031/2013.20684 [26] ZHANG J Y, LI Y, XUAN G X, et al. Overtopping breaching of cohesive homogeneous earth dam with different cohesive strength[J]. Science in China Series E: Technological Sciences, 2009, 52(10): 3024-3029. doi: 10.1007/s11431-009-0275-1 [27] RITTER A. Die fortpflanzung von wasserwellen (propagation of water waves)[J]. Zeitschrift Verein Deutscher Ingenieure, 1892, 36(2): 947-954. [28] DRESSLER R F. Hydraulic resistance effect upon the dam-break functions[J]. Journal of Research of the National Bureau of Standards, 1952, 49(3): 217. doi: 10.6028/jres.049.021 [29] DRESSLER R F. Unsteady non-linear waves in sloping channels[J]. Proceedings of the Royal Society of London Series A, Mathematical and Physical Sciences, 1958, 247(1249): 186-198. doi: 10.1098/rspa.1958.0177 [30] STOKER J J. Water waves: The mathematical theory with applications[M]. New York: John Wiley & Sons, 1992. [31] CASTRO-ORGAZ O, CHANSON H. Ritter's dry-bed dam-break flows: Positive and negative wave dynamics[J]. Environmental Fluid Mechanics, 2017, 17(4): 665-694. [32] 伍超. 梯形断面溃坝波Ritter解[J]. 水动力学研究与进展, 1986, 1(2): 82-88. doi: 10.16076/j.cnki.cjhd.1986.02.010WU C. Ritter's solution of dam-breaking wave in trapezoid cross-section channel[J]. Journal of Hydrodynamics, 1986, 1(2): 82-88. (in Chinese with English abstract doi: 10.16076/j.cnki.cjhd.1986.02.010 [33] 宁利中. 椭圆形断面溃坝波Ritter解[J]. 西安理工大学学报, 1990, 6(4): 283-291. doi: 10.19322/j.cnki.issn.1006-4710.1990.04.008NING L Z. Ritter's solution of dam-breaking wave in elliptic cross-section channel[J]. Journal of Xi'an University of Technology, 1990, 6(4): 283-291. (in Chinese with English abstract doi: 10.19322/j.cnki.issn.1006-4710.1990.04.008 [34] 谢任之. 溃坝坝址流量计算[J]. 水利水运科学研究, 1982(1): 43-58.XIE R Z. Computation for the discharge from the site of dam-break[J]. Hydro-Science and Engineering, 1982(1): 43-58. (in Chinese with English abstract [35] 谢任之. 溃坝水力学[M]. 济南: 山东科学技术出版社, 1993.XIE R Z. Dam-break hydraulics[M]. Jinan: Shandong Science & Technology Press, 1993. (in Chinese) [36] 宁利中, 宁碧波, 胡彪, 等. 任意梯形断面溃坝洪水最大流量解析解[J]. 西安理工大学学报, 2017, 33(2): 164-168. doi: 10.19322/j.cnki.issn.1006-4710.2017.02.007NING L Z, NING B B, HU B, et al. Analytical solutions to maximum discharge of dam-breaking flood in arbitrary trapezoidal cross-section channels[J]. Journal of Xi'an University of Technology, 2017, 33(2): 164-168. (in Chinese with English abstract doi: 10.19322/j.cnki.issn.1006-4710.2017.02.007 [37] CHEN T K, CAPART H. Kinematic wave solutions for dam-break floods in non-uniform valleys[J]. Journal of Hydrology, 2020, 582: 124381. doi: 10.1016/j.jhydrol.2019.124381 [38] WANG B, CHEN Y L, PENG Y, et al. Analytical solution of shallow water equations for ideal dam-break flood along a wet-bed slope[J]. Journal of Hydraulic Engineering, 2020, 146(2): 06019020. [39] KIRKPATRICK G W. Evaluation guidelines for spillway adequacy[C]//Anon. Proceedings of the Engineering Foundation Conference. [S. l. ]: [s. l. ], 1977. [40] FROEHLICH D C. Predicting peak discharge from gradually breached embankment dam[J]. Journal of Hydrologic Engineering, 2016, 21(11): 04016041. doi: 10.1061/(ASCE)HE.1943-5584.0001424 [41] Soil Conservation Service. Simplified dan-breach routing procedure[R]. Washington DC: US Dept. of Agriculture, 1981. [42] HAGEN V K. Re-evaluation of design floods and dam safety[C]//Anon. Proceedings of the 14th Congress of the International Commission on Large Dams. [S. l. ]: [s. l. ], 1982. [43] SINGH K P, SNORRASON A. Sensitivity of outflow peaks and flood stages to the selection of dam breach parameters and simulation models[J]. Journal of Hydrology, 1984, 68(1/2/3/4): 295-310. doi: 10.1016/0022-1694(84)90217-8 [44] MACDONALD T C, LANGRIDGE-MONOPOLIS J. Breaching charateristics of dam failures[J]. Journal of Hydraulic Engineering, 1984, 110(5): 567-586. doi: 10.1061/(ASCE)0733-9429(1984)110:5(567) [45] COSTA J E. Floods from dam failures[R]. Denver: USGS, 1985: 5-560. [46] EVANS S G. The maximum discharge of outburst floods caused by the breaching of man-made and natural dams[J]. Canadian Geotechnical Journal, 1986, 23(3): 385-387. doi: 10.1139/t86-053 [47] U. S. Bureau of Reclamation. Downstream hazard classification guidelines[R]. Denver: U. S. Department of the Interior, 1988. [48] FROEHLICH D C. Peak outflow from breached embankment dam[J]. Journal of Water Resources Planning and Management, 1995, 121(1): 90-97. doi: 10.1061/(ASCE)0733-9496(1995)121:1(90) [49] WALDER J S, O'CONNOR J E. Methods for predicting peak discharge of floods caused by failure of natural and constructed earthen dams[J]. Water Resources Research, 1997, 33(10): 2337-2348. doi: 10.1029/97WR01616 [50] XU Y, ZHANG L M. Breaching parameters for earth and rockfill dams[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(12): 1957-1970. doi: 10.1061/(ASCE)GT.1943-5606.0000162 [51] PIERCE M W, THORNTON C I, ABT S R. Predicting peak outflow from breached embankment dams[J]. Journal of Hydrologic Engineering, 2010, 15(5): 338-349. doi: 10.1061/(ASCE)HE.1943-5584.0000197 [52] THORNTON C I, PIERCE M W, ABT S R. Enhanced predictions for peak outflow from breached embankment dams[J]. Journal of Hydrologic Engineering, 2011, 16(1): 81-88. doi: 10.1061/(ASCE)HE.1943-5584.0000288 [53] PENG M, ZHANG L M. Breaching parameters of landslide dams[J]. Landslides, 2012, 9(1): 13-31. doi: 10.1007/s10346-011-0271-y [54] DE LORENZO G, MACCHIONE F. Formulas for the peak discharge from breached earthfill dams[J]. Journal of Hydraulic Engineering, 2014, 140(1): 56-67. doi: 10.1061/(ASCE)HY.1943-7900.0000796 [55] HOOSHYARIPOR F, TAHERSHAMSI A, GOLIAN S. Application of copula method and neural networks for predicting peak outflow from breached embankments[J]. Journal of Hydro-Environment Research, 2014, 8(3): 292-303. doi: 10.1016/j.jher.2013.11.004 [56] AZIMI R, VATANKHAH A R, KOUCHAKZADEH S. Predicting peak discharge from breached embankment dams[C]//Anon. 36th IAHR World Congress. [S. l. ]: [s. l. ], 2015. [57] 黄委会科研所. 溃坝水流计算方法初步探讨[J]. 水利科技情报, 1976.Henan Yellow River Commission Research Institute. Preliminary study on the calculation method of dam break water flow[M]. Hydraulic Science and Technology Information, 1976. (in Chinese with English abstract [58] 戴荣尧, 王群. 溃坝最大流量的研究[J]. 水利学报, 1983, 14(2): 13-21.DAI R Y, WANG Q. Research on the maximum discharge of dam-breaking[J]. Journal of Hydraulic Engineering, 1983, 14(2): 13-21. (in Chinese with English abstract [59] 国家防汛抗旱总指挥部, 水利部水利水电规划设计总院, 中国水利水电科学研究院. 洪水风险图编制技术细则(试行)[S]. 北京: 国家防汛抗旱总指挥部, 2013.The State Flood Control and Drought Relief Headquarters, China Institute of Water Resources Planning and Design, China Institute of Water Resources and Hydropower Research. Detailed rules for the compilation of flood hazard maps (trial)[S]. Beijing: The State Flood Control and Drought Relief Headquarters, 2013. (in Chinese) [60] 邓刚, 赵博超, 温彦锋, 等. 土石坝漫顶溃口洪水过程概化计算模型[C]//佚名. 高坝建设与运行管理的技术进展: 中国大坝协会2014学术年会论文集. [出版地未知]: [出版者未知], 2014: 337-342.DENG G, ZHAO B C, WEN Y F, et al. Generalized calculation model of flood process for earthen dam overtopping failure[C]//Anon. Technical Progress in the Construction and Operation Management of High Dams: Proceedings of the 2014 Academic Annual Meeting of the China Large Dam Association. [S. l. ]: [s. l. ], 2014: 337-342. (in Chinese) [61] 石振明, 马小龙, 彭铭, 等. 基于大型数据库的堰塞坝特征统计分析与溃决参数快速评估模型[J]. 岩石力学与工程学报, 2014, 33(9): 1780-1790. doi: 10.13722/j.cnki.jrme.2014.09.007SHI Z M, MA X L, PENG M, et al. Statistical analysis and efficient dam burst modelling of landslide dams based on a large-scale database[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1780-1790. (in Chinese with English abstract doi: 10.13722/j.cnki.jrme.2014.09.007 [62] 梅世昂, 陈生水, 钟启明, 等. 土石坝溃坝参数模型研究[J]. 工程科学与技术, 2018, 50(2): 60-66. doi: 10.15961/j.jsuese.201700828MEI S A, CHEN S S, ZHONG Q M, et al. Parametric model for breaching analysis of earth-rock dam[J]. Advanced Engineering Sciences, 2018, 50(2): 60-66. (in Chinese with English abstract doi: 10.15961/j.jsuese.201700828 [63] 齐子杰, 黄卫, 汪利先, 等. 堰塞坝溃决参数模型评估与优化分析[J]. 人民长江, 2022, 53(12): 157-166. doi: 10.16232/j.cnki.1001-4179.2022.12.024QI Z J, HUANG W, WANG L X, et al. Evaluation and optimization analysis of barrier dam breach parameter models[J]. Yangtze River, 2022, 53(12): 157-166. (in Chinese with English abstract doi: 10.16232/j.cnki.1001-4179.2022.12.024 [64] 单熠博, 陈生水, 钟启明, 等. 考虑颗粒组成的堰塞体溃口峰值流量快速预测模型[J]. 应用基础与工程科学学报, 2023, 31(3): 584-598. doi: 10.16058/j.issn.1005-0930.2023.03.005SHAN Y B, CHEN S S, ZHONG Q M, et al. A rapid prediction model for peak breach flow of landslide dams considering the grain composition of deposits[J]. Journal of Basic Science and Engineering, 2023, 31(3): 584-598. (in Chinese with English abstract doi: 10.16058/j.issn.1005-0930.2023.03.005 [65] FROEHLICH D C. Peak flood discharge from a landslide dam outburst[J]. Natural Hazards Review, 2022, 23(2): 04022001. doi: 10.1061/(ASCE)NH.1527-6996.0000545 [66] 焦煦, 冯震宇, 廖海梅. 堰塞坝溃口及洪峰参数模型评估与优化[J]. 贵州大学学报(自然科学版), 2023, 40(5): 87-95. doi: 10.15958/j.cnki.gdxbzrb.2023.05.11JIAO X, FENG Z Y, LIAO H M. Evaluation and optimization of landslide dam breaking and flood peak parameter models[J]. Journal of Guizhou University (Natural Sciences), 2023, 40(5): 87-95. (in Chinese with English abstract doi: 10.15958/j.cnki.gdxbzrb.2023.05.11 [67] GUAN S G, SHI Z M, ZHENG H C, et al. Effects of soil properties and geomorphic parameters on the breach mechanisms of landslide dams and prediction of peak discharge[J]. Acta Geotechnica, 2023, 18(10): 5485-5502. doi: 10.1007/s11440-023-01908-2 [68] 冯震宇, 杨兴国, 周家文, 等. 堰塞坝溃决参数及其寿命预测[J]. 水利学报, 2024, 55(3): 367-377. doi: 10.13243/j.cnki.slxb.20230368FENG Z Y, YANG X G, ZHOU J W, et al. Estimation of breach parameters and longevity of landslide dam[J]. Journal of Hydraulic Engineering, 2024, 55(3): 367-377. (in Chinese with English abstract doi: 10.13243/j.cnki.slxb.20230368 [69] VONTHUN J L, GILLETTE D R. Guidance on breach parameters[Z]. Denver Colorado: U. S. Bureau of Reclamation, 1990. [70] 刘建康, 程尊兰, 吴积善. 基于经验公式建立的滑坡泥石流坝溃口形式预测模型[J]. 四川大学学报(工程科学版), 2013, 45(增刊2): 84-89.LIU J K, CHENG Z L, WU J S. An empirical model calculating the breach parameters of landslide and debris-flow dam[J]. Journal of Sichuan University(Engineering Science Edition), 2013, 45(S2): 84-89. (in Chinese with English abstract [71] 张昕健, 渠庚, 范北林, 等. 溃堤洪水与堤后冲刷研究综述及展望[J]. 长江科学院院报, 2019, 36(4): 9-12. doi: 10.11988/ckyyb.20171143ZHANG X J, QU G, FAN B L, et al. Study on dike-break flood and scouring: Review and prospect[J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(4): 9-12. (in Chinese with English abstract doi: 10.11988/ckyyb.20171143 [72] 张新华, 薛睿瑛, 王明, 等. 堰塞坝溃口演化研究进展[J]. 西南民族大学学报(自然科学版), 2020, 46(1): 85-91. doi: 10.11920/xnmdzk.2020.01.013ZHANG X H, XUE R Y, WANG M, et al. Research progress on the breach-evolution of natural dams[J]. Journal of Southwest Minzu University (Natural Science Edition), 2020, 46(1): 85-91. (in Chinese with English abstract doi: 10.11920/xnmdzk.2020.01.013 [73] 谢亚军, 朱勇辉, 国小龙. 土坝溃决研究进展及存在问题[J]. 长江科学院院报, 2013, 30(4): 29-33. doi: 10.3969/j.issn.1001-5485.2013.04.007XIE Y J, ZHU Y H, GUO X L. Advances and problems in earth-dam failure research[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(4): 29-33. (in Chinese with English abstract doi: 10.3969/j.issn.1001-5485.2013.04.007 [74] FREAD D L. DAMBRK: The NWS dam break flood forecasting model[R]. Silver Spring: National Weather Service(NWS), NOAA, 1984. [75] CRISTOFANO E A. Method of computing erosion rate for failure of earth-fill dams[R]. Denver: Bureau of Reclamation, 1965. [76] HARRIS G W, WAGNER D A. Outflow from breached earth dams[R]. Salt Lake City: Department of Civil Engineering, University of Utah, 1967. [77] BROWN R J, ROGERS D C. BRDAM users manual [M]. Denve: Water and Power Resources Service, U. S. Department of the Interior, 1981. [78] LOU W C. Mathematical modeling of earth dam breaches[D]. Fort Collins: Colorado State University, 1981. [79] PONCE V M, TSIVOGLOU A J. Modeling gradual dam breaches[J]. Journal of Hydraulic Division(ASCE), 1981, 107(7): 829-838. doi: 10.1061/jyceaj.0005694 [80] NOGUEIRA V D Q. A mathematical model of progressive earth dam failure[D]. Fort Collins: Colorado State University, 1984. [81] SINGH V P, QUIROGA C A. Dimensionless analytical solutions for dam-breach erosion[J]. Journal of Hydraulic Research, 1988, 26(2): 179-197. doi: 10.1080/00221688809499224 [82] FREAD D L. BREACH: An erosion model for earthen dam failures[R]. Silver Spring: National Weather Service(NWS) Report, MA NOAA, 1988. [83] FREAD D L. BREACH: NWS FLDWAV model[R]. Silver Spring: National Weather Service(NWS), MA NOAA, 1998. [84] FROEHLICH D C. Two dimensional model for embankment dam breach formation and flood wave generation[C]//Association of State Dam Safety Officials. 2004 Conference of ASDSO. [S. l. ]: [s. l. ], 2004. [85] ZHU Y H, VISSER P J, VRIJLING J K. A model for breach erosion in clay-dikes[C]//Anon. Coastal Dynamics 2005. Barcelona, Spain: American Society of Civil Engineers, 2006: 1-10. [86] WU W M, KANG Y, WANG S S Y. An earthen embankment breach model[C]∥IAHR. Proceedings of the 33rd Congress of IAHR(CD-ROM). [S. l. ]: [s. l. ], 2009. [87] CAO Z X, YUE Z Y, PENDER G. Landslide dam failure and flood hydraulics. Part Ⅱ: Coupled mathematical modelling[J]. Natural Hazards, 2011, 59(2): 1021-1045. [88] CHEN Z Y, MA L Q, YU S, et al. Back analysis of the draining process of the Tangjiashan barrier lake[J]. Journal of Hydraulic Engineering, 2015, 141(4): 05014011. doi: 10.1061/(ASCE)HY.1943-7900.0000965 [89] ANDREW D P, COLEMAN S E, WEBBY M G, et al. Noncohesive embankment failure due to overtopping flow[C]//Anon. 28th Congress of the Int. Association for Hydraulic Research. [S. l. ]: [s. l. ], 1998. [90] LOUKOLA E, HUOKUNA M. A numerical erosion model for embankment dams failure and its use for risk assessment[R]. Munich: Lockeed Company, 1998. [91] VISSER P J. Breach growth in sand-dikes[D]. Delft: Delft University of Technology, 1998. [92] MOHAMED M A, SAMUELS P G, MORRIS M W, et al. Improving the accuracy of prediction of breach formation through embankment dams and flood embankments[J]. Engineering, Environmental Science, 2004: 41538804. [93] TEMPLE D M, HANSON G J, NEILSEN M L, et al. Simplified breach analysis model for homogeneous embankments. Part I: Background and model components[C]//Anon. Proceedings of the 2005 US Society on Dams Annual Meeting and Conference. [S. l. ]: [s. l. ], 2005: 151-161. [94] TEMPLE D M, HANSON G J, NEILSEN M L. WINDAM: Analysis of overtopped earth embankment dams[C]//Anon. 2006 American Society of Agricultural and Biological Engineers. [S. l. ]: [s. l. ], 2006: 062105. [95] 陈生水, 钟启明, 任强. 土石坝漫顶破坏溃口发展数值模型研究[J]. 水利水运工程学报, 2009(4): 53-58. doi: 10.3969/j.issn.1009-640X.2009.04.007CHEN S S, ZHONG Q M, REN Q. Numerical model study on break development due to overtopping failure for earth-rock dam[J]. Hydro-Science and Engineering, 2009(4): 53-58. (in Chinese with English abstract doi: 10.3969/j.issn.1009-640X.2009.04.007 [96] 傅旭东, 刘帆, 马宏博, 等. 基于物理模型的唐家山堰塞湖溃决过程模拟[J]. 清华大学学报(自然科学版), 2010, 50(12): 1910-1914. doi: 10.16511/j.cnki.qhdxxb.2010.12.008FU X D, LIU F, MA H B, et al. Physically based simulation of the breaching of the Tangjiashan quake lake[J]. Journal of Tsinghua University (Science and Technology), 2010, 50(12): 1910-1914. (in Chinese with English abstract doi: 10.16511/j.cnki.qhdxxb.2010.12.008 [97] OSMAN A M, THORNE C R. Riverbank stability analysis. I: Theory[J]. Journal of Hydraulic Engineering, 1988, 114(2): 134-150. [98] CHANG D S, ZHANG L M. Simulation of the erosion process of landslide dams due to overtopping considering variations in soil erodibility along depth[J]. Natural Hazards and Earth System Sciences, 2010, 10(4): 933-946. doi: 10.5194/nhess-10-933-2010 [99] DHI Water Environment. A modelling system for rivers and channels user guide[Z]. CO, California: DHI Group, 2012. [100] WU W M. Simplified physically based model of earthen embankment breaching[J]. Journal of Hydraulic Engineering, 2013, 139(8): 837-851. doi: 10.1061/(ASCE)HY.1943-7900.0000741 [101] BRUNNER G W. HEC-RAS river analysis system: Hydraulic reference manua, version 5.0[M]. Vicksburg, Mississippi: US Army Corps of Engineers-Hydrologic Engineering Center, 2016: 547. [102] ZHAO G. Breach growth in cohesive embankments due to overtopping[M]. Delf: Delft Academic Press. 2016. [103] 沈鸿杰, 徐力群, 刘子茜. 改进DB-IWHR模型及其在尾矿库溃坝影响分析中的应用[J]. 水利水电科技进展, 2022, 42(5): 64-70. doi: 10.3880/j.issn.10067647.2022.05.010SHEN H J, XU L Q, LIU Z X. Improved DB-IWHR model and its application in influence analysis of tailings dam break[J]. Advances in Science and Technology of Water Resources, 2022, 42(5): 64-70. (in Chinese with English abstract doi: 10.3880/j.issn.10067647.2022.05.010 [104] 巨江, 贺翠玲, 李鹏峰. 堰塞湖土石坝漫顶溃坝扩散模型[J]. 泥沙研究, 2024, 49(5): 1-8. doi: 10.16239/j.cnki.0468-155x.2024.05.001JU J, HE C L, LI P F. Diffusion model of overtopping dam-break process in earth-rock barrier dam[J]. Journal of Sediment Research, 2024, 49(5): 1-8. (in Chinese with English abstract doi: 10.16239/j.cnki.0468-155x.2024.05.001 [105] 吕佳豪, 侯精明, 李东来, 等. 溃坝洪水演进一维水动力模型[J]. 山地学报, 2024, 42(1): 123-131. doi: 10.16089/j.cnki.1008-2786.000809LYU J H, HOU J M, LI D L, et al. One-dimensional hydrodynamic model for dam-break flooding[J]. Mountain Research, 2024, 42(1): 123-131. (in Chinese with English abstract doi: 10.16089/j.cnki.1008-2786.000809 [106] 陈淑婧, 王秋生, 于沭, 等. 土石坝漫顶溃决模型的分析比较[J]. 河海大学学报(自然科学版), 2016, 44(5): 406-411. doi: 10.3876/j.issn.1000-1980.2016.05.005CHEN S J, WANG Q S, YU S, et al. Comparative analysis of models for overtopping-induced earth-rock dam breach[J]. Journal of Hohai University (Natural Sciences), 2016, 44(5): 406-411. (in Chinese with English abstract doi: 10.3876/j.issn.1000-1980.2016.05.005 [107] 王乃欣. 土石坝溃决溃口数值模拟与溃坝虚拟现实技术研究[D]. 北京: 中国水利水电科学研究院, 2018.WANG N X. Research on modeling lateral enlargement in dam breach and virtual reality technology of earth dam[D]. Beijing: China Institute of Water Resources and Hydropower Research, 2018. (in Chinese with English abstract [108] CLARKSON L, WILLIAMS D. An overview of conventional tailings dam geotechnical failure mechanisms[J]. Mining, Metallurgy & Exploration, 2021, 38(3): 1305-1328. [109] CHEN Z Y, PING Z Y, WANG N X, et al. An approach to quick and easy evaluation of the dam breach flood[J]. Science China Technological Sciences, 2019, 62(10): 1773-1782. doi: 10.1007/s11431-018-9367-4 [110] CHEN S, FANG X, ZHONG Q, et al. Centrifugal model tests and numerical simulations for break of earth-rock dams due to overtopping[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 922-932. [111] 钟启明, 陈生水, 邓曌. 堰塞坝漫顶溃决机理与溃坝过程模拟[J]. 中国科学: 技术科学, 2018, 48(9): 959-968.ZHONG Q M, CHEN S S, DENG Z. Breach mechanism and numerical modeling of barrier dam due to overtopping failure[J]. Scientia Sinica (Technologica), 2018, 48(9): 959-968. (in Chinese with English abstract [112] LIU F, FU X D, WANG G Q, et al. Physically based simulation of dam breach development for Tangjiashan quake dam, China[J]. Environmental Earth Sciences, 2012, 65(4): 1081-1094. doi: 10.1007/s12665-011-1025-9 [113] 邵学军, 王兴奎. 河流动力学概论[M]. 北京: 清华大学出版社, 2013.SHAO X J, WANG X K. Introduction to river mechanics[M]. Beijing: Tsinghua University Press, 2013.(in Chinese) -
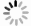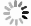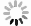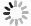



 下载:
下载: