Determination of the 3D most dangerous sliding surface for open-pit mine slopes based on multiple cross-profiles
-
摘要:
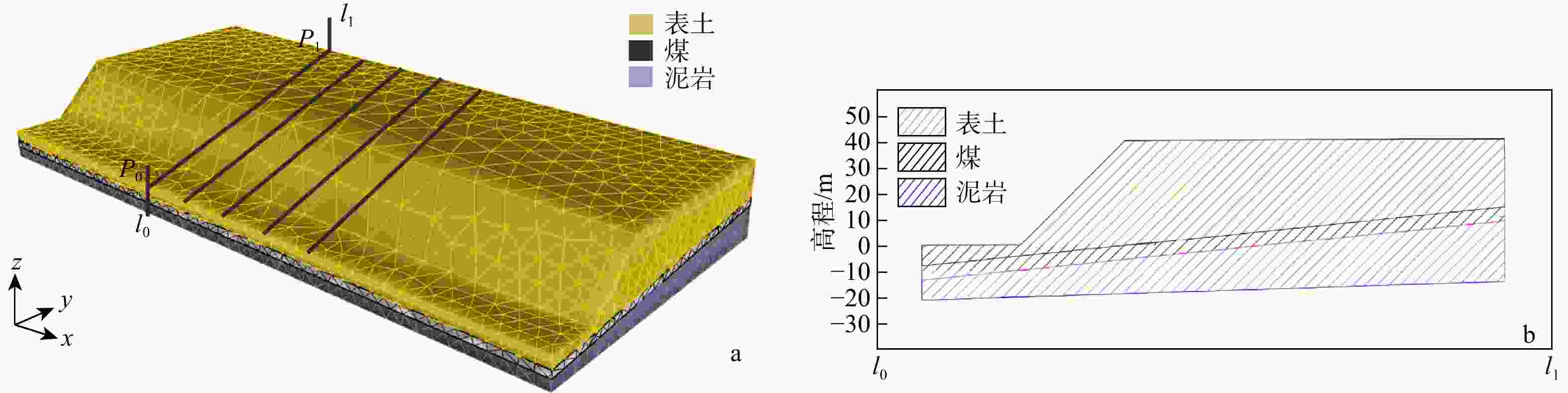
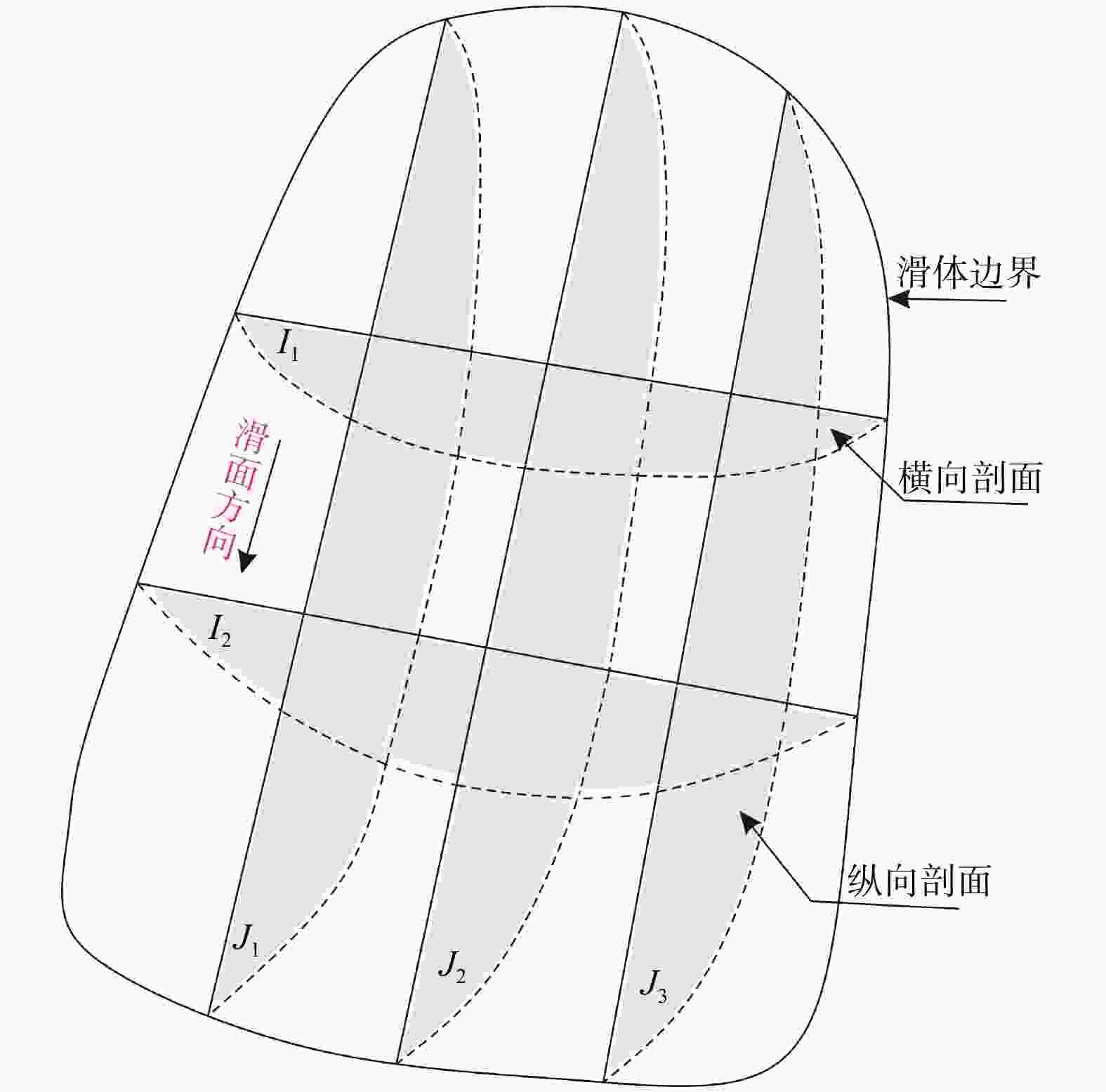
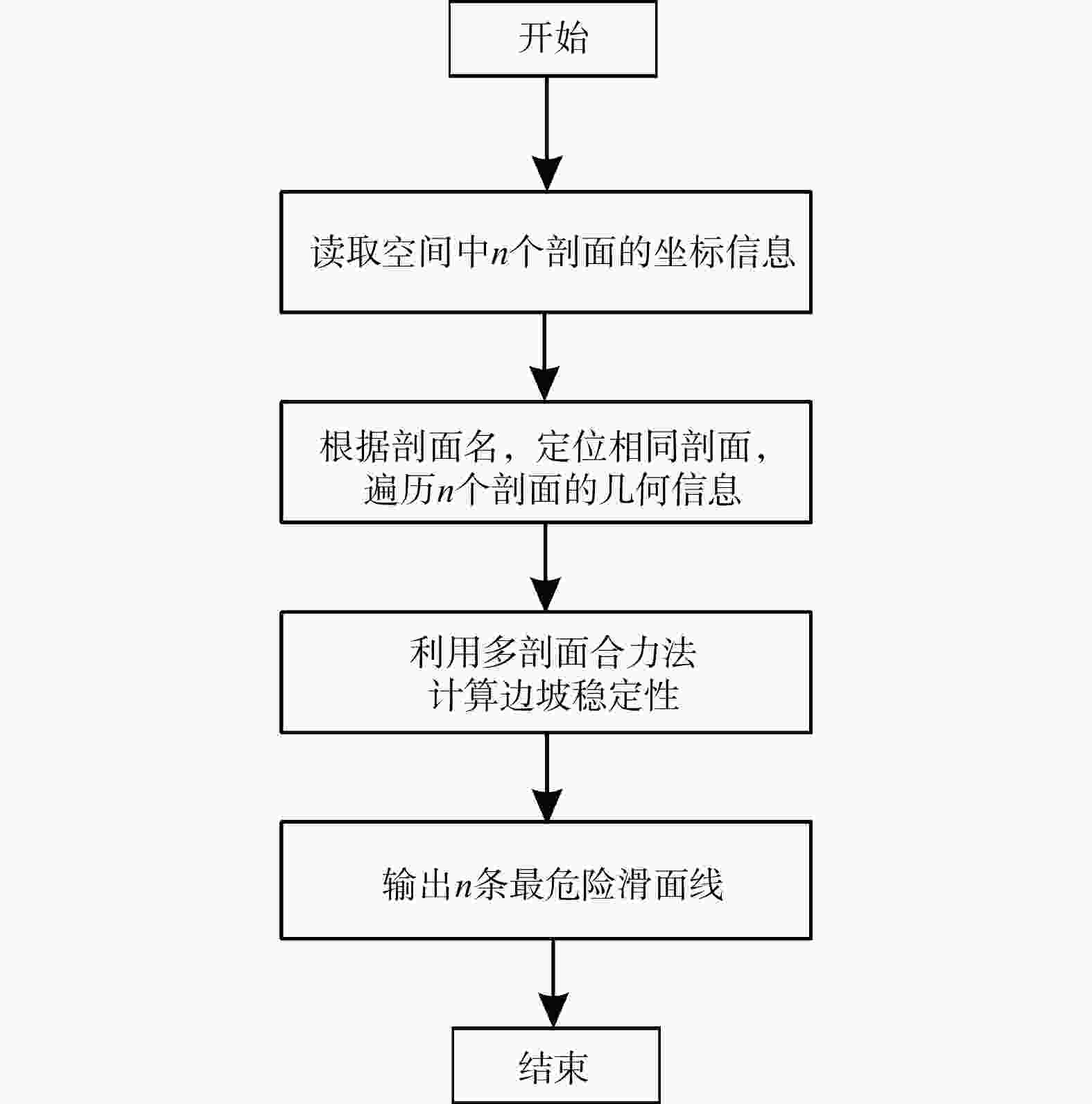
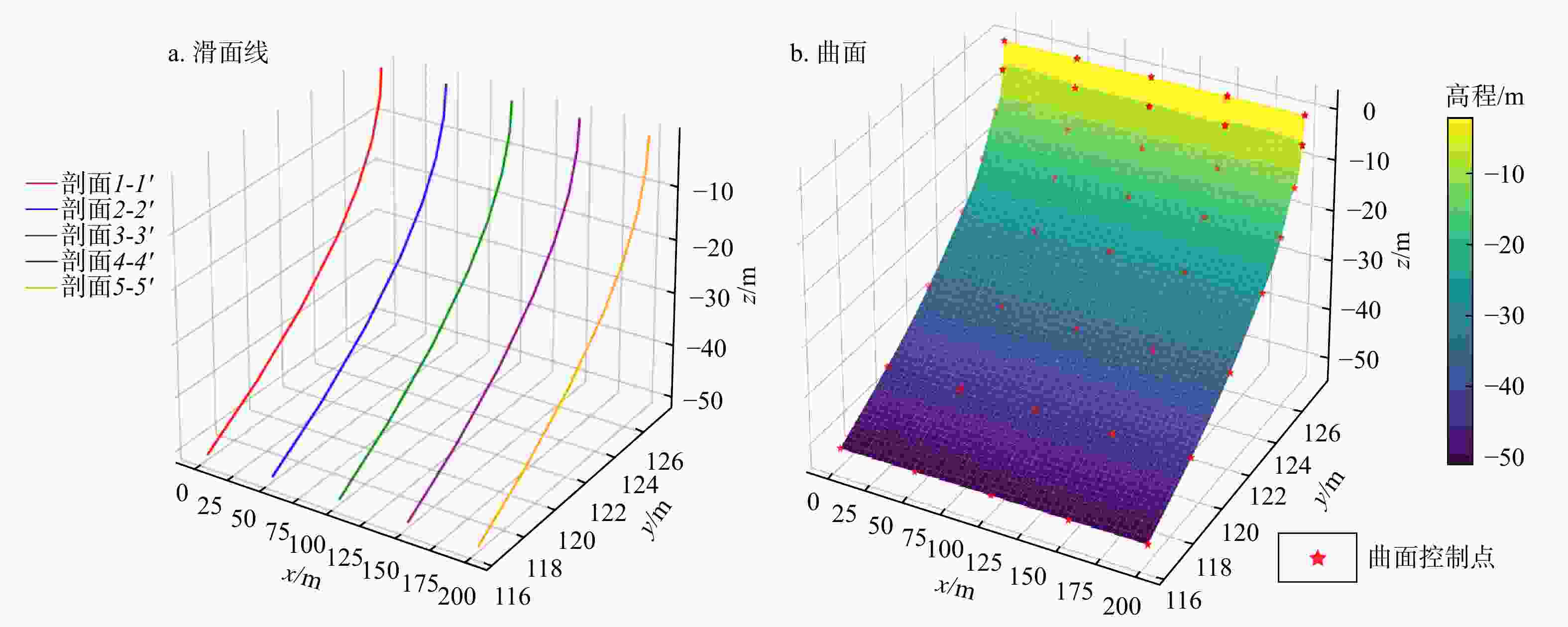
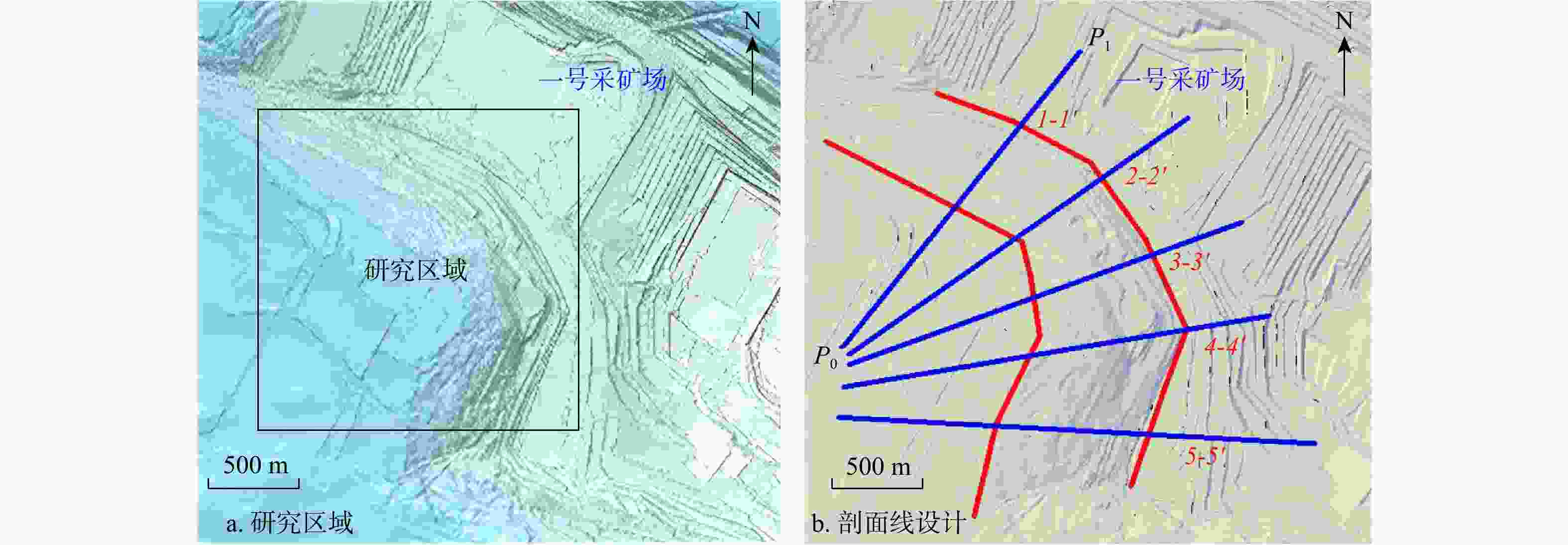
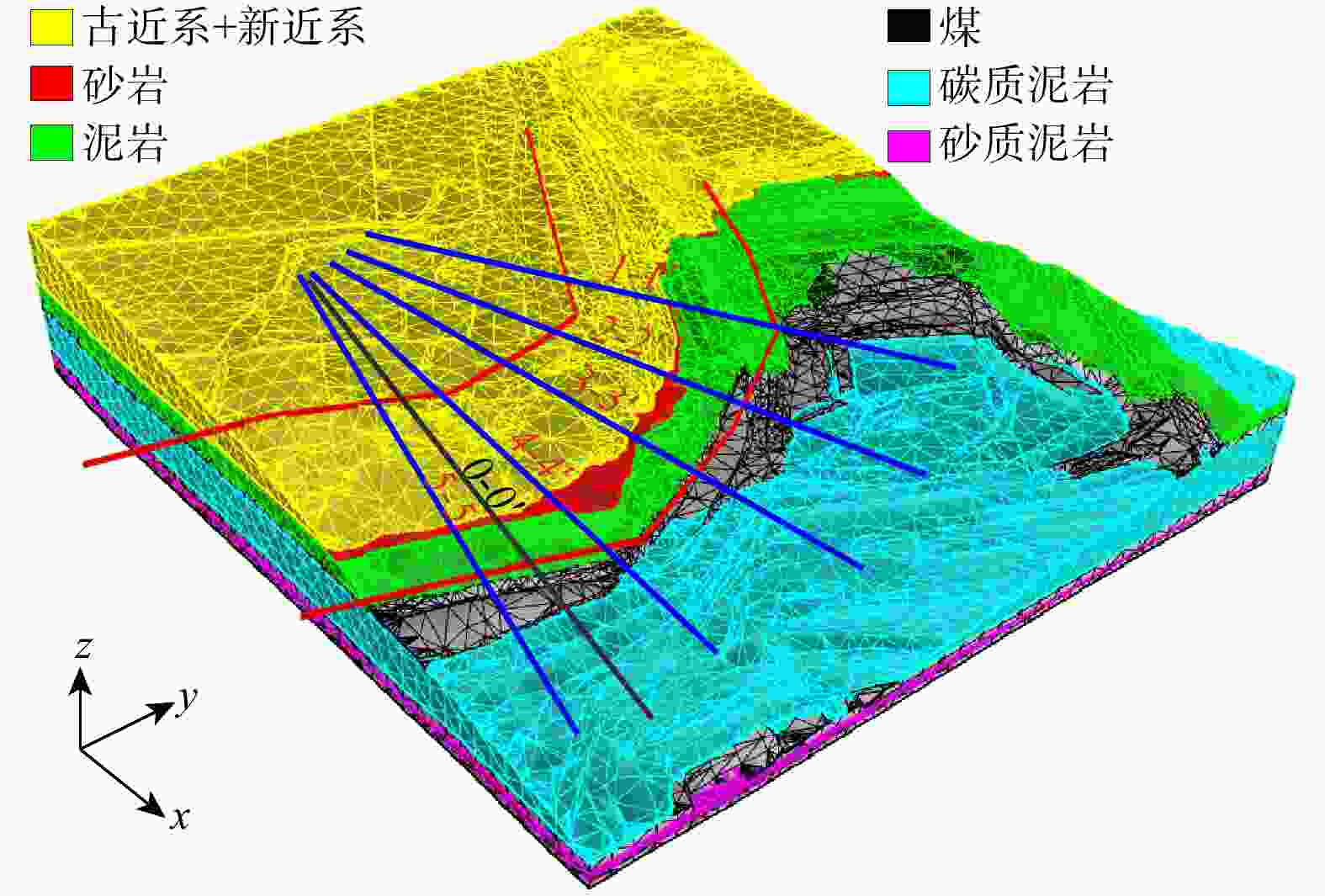
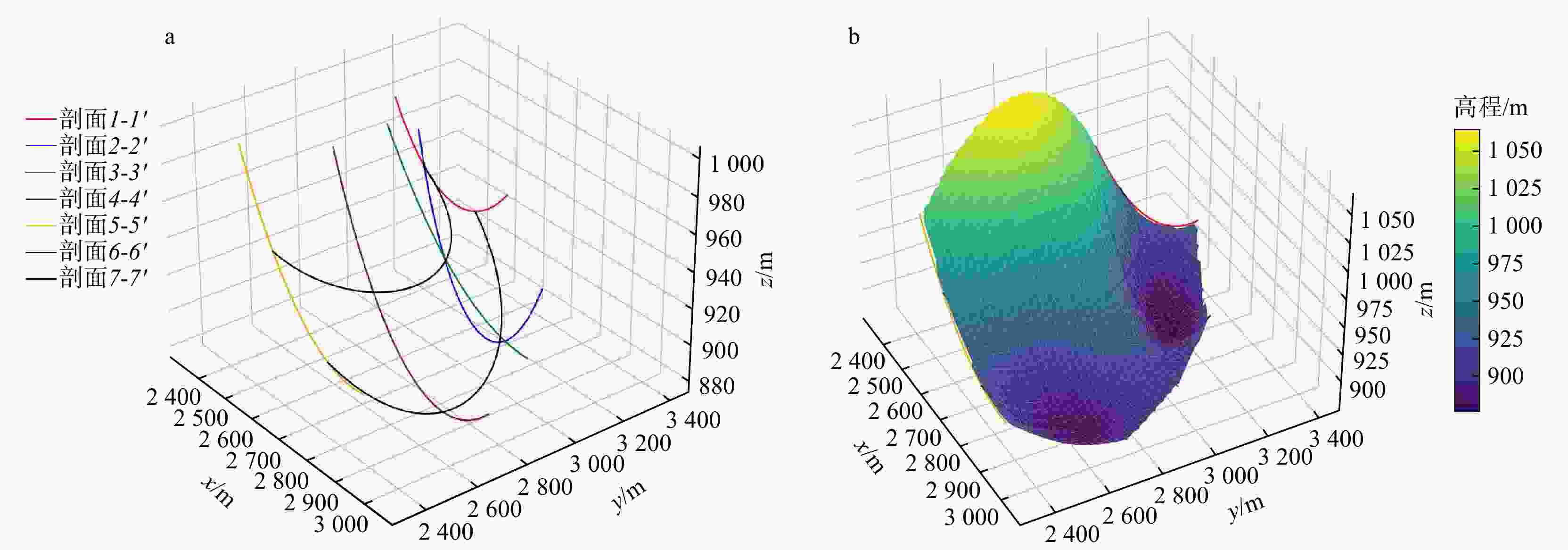
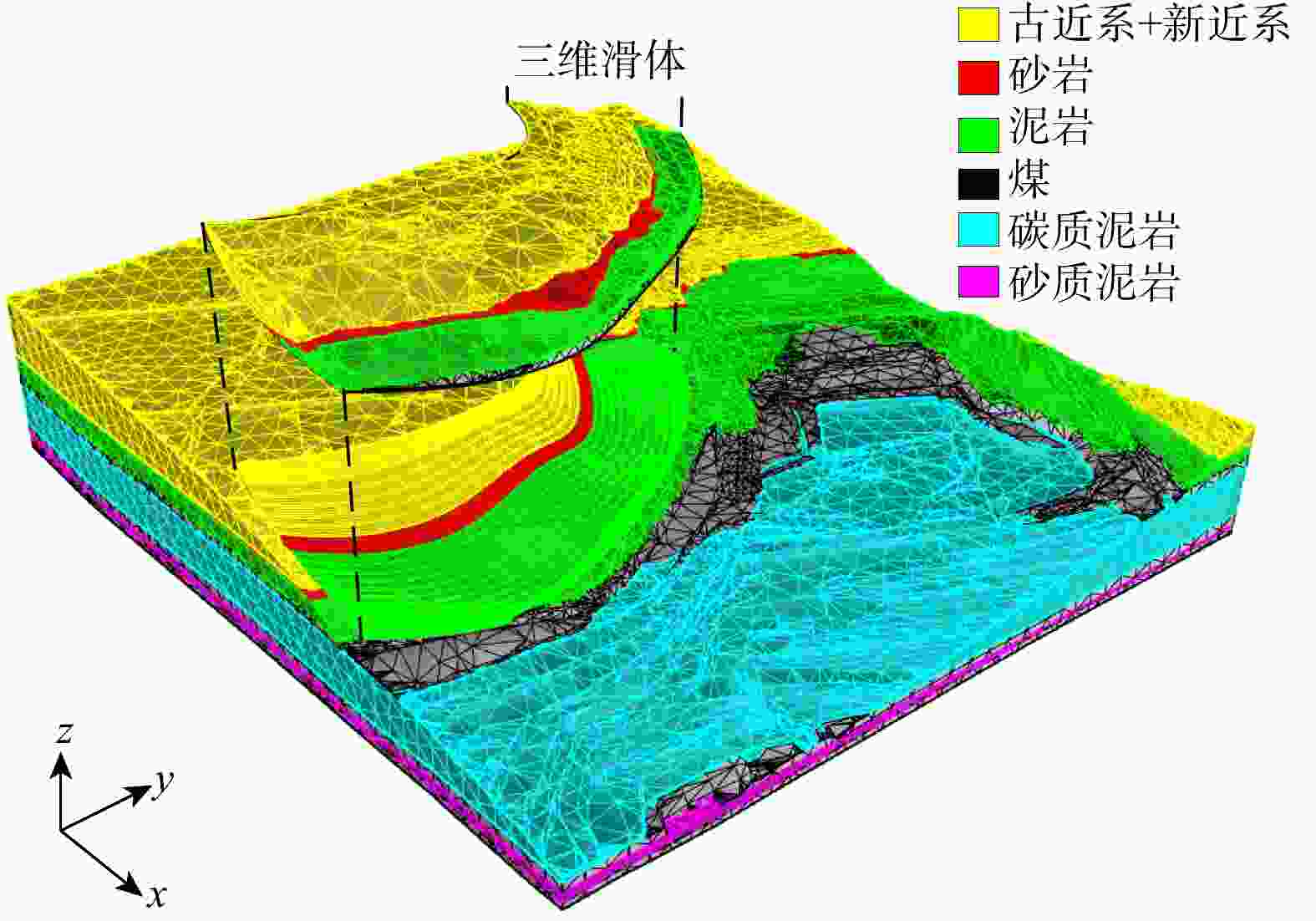
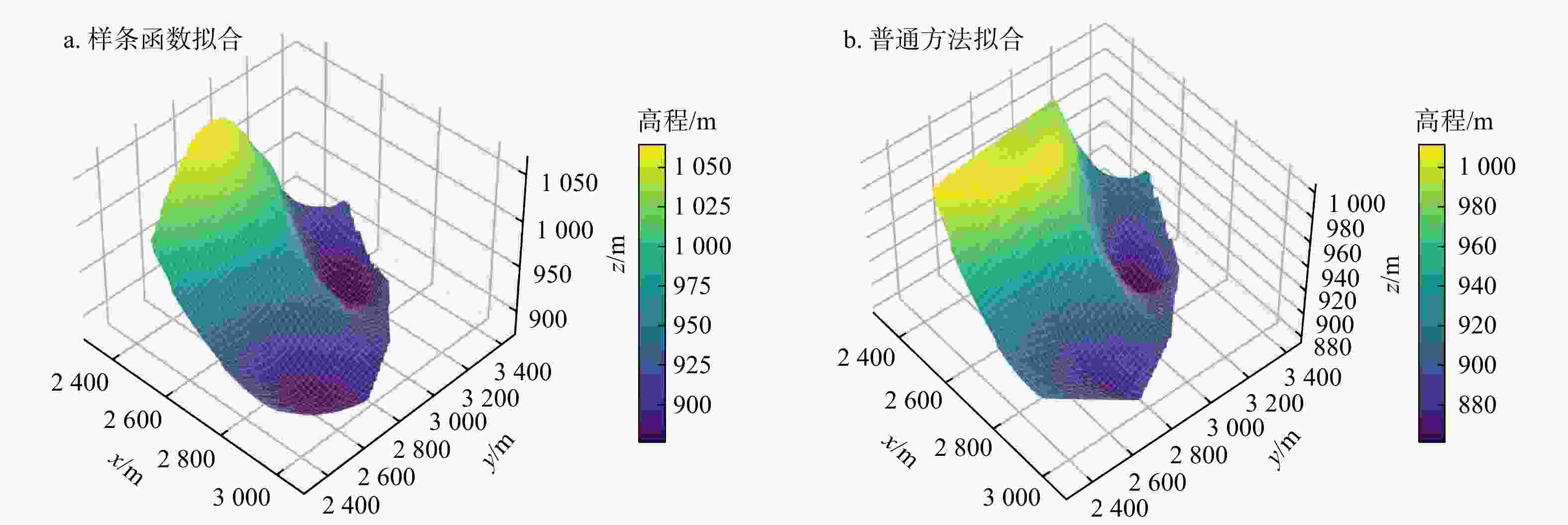
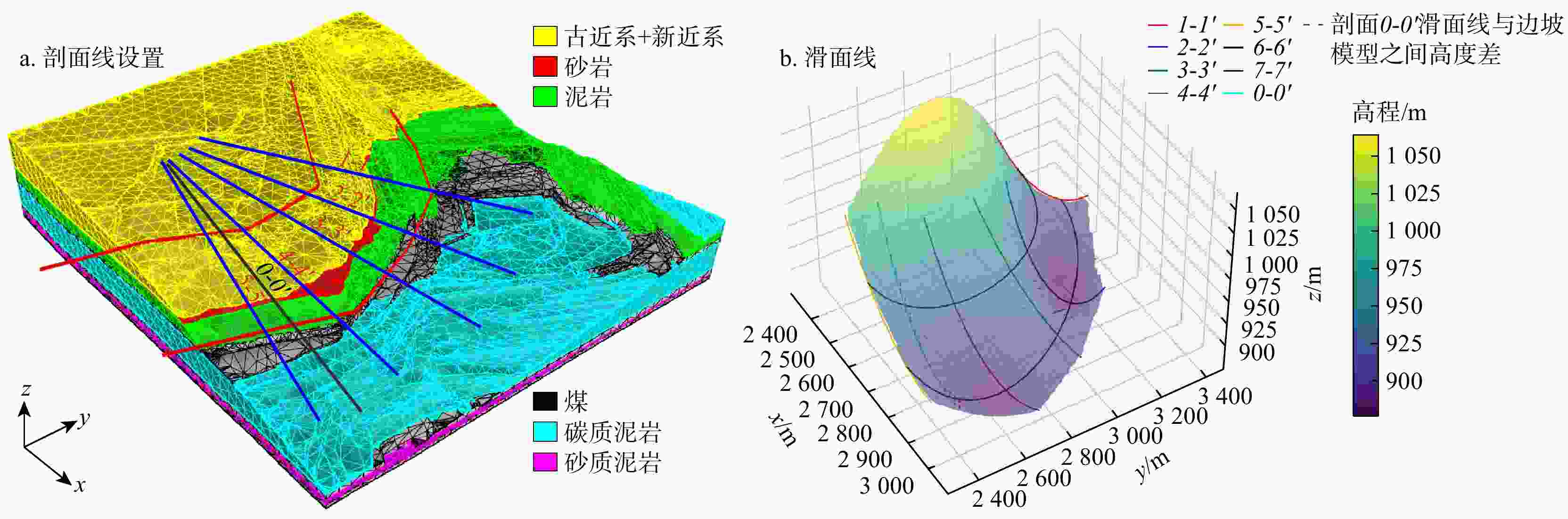
目前，普遍采用二维剖面进行边坡稳定性分析，该方法能高效且较为准确地评估边坡的稳定性。然而，二维剖面不能描述边坡最危险滑面的三维空间形态和三维滑体。为解决此问题，在二维剖面边坡稳定性分析的基础上，通过将多个剖面与三维边坡模型进行关联，使用样条函数拟合出边坡三维最危险滑面。首先，通过设置剖面线和二维剖面图中图元的剖面名称、水平坐标定位及高程定位，建立了二维剖面图与三维边坡空间的关联；其次，利用多剖面合力法分别自动生成了各剖面的最危险滑面线，使用坐标转换公式将每个二维剖面的最危险滑面线转换到三维边坡空间；最后，利用样条函数插值，成功生成了该边坡的三维最危险滑面。以内蒙古锡林浩特某露天矿西南帮边坡为例，建立了边坡三维工程地质模型，生成了5个边坡稳定性分析二维剖面，通过该方法成功生成了该边坡的三维最危险滑面及三维滑体并验证了其合理性。研究成果为预估潜在边坡滑体位置、规模和破坏程度提供了新的思路。
Abstract:At present, the two-dimensional (2D) profiles are widely used for slope stability analysis, which has proved to be efficient and relatively accurate.
ObjectiveHowever, the two-dimensional profile cannot describe the 3D spatial morphology of the most dangerous sliding surface sliding mass.
Methods and ResultsTo address the limitation, based on the stability analysis of the two-dimensional profile slope, the three-dimensional most dangerous sliding surface of the slope is fitted using the spline function by associating multiple profiles with the three-dimensional slope model. Firstly, the relationship between the two-dimensional profile and the three-dimensional slope space is established by setting the profile name, horizontal coordinate positioning and elevation positioning of the graphic elements in the profile line and the two-dimensional profile. Secondly, the most dangerous sliding surface lines of each profile are automatically generated by using the multi-profile resultant force method, and the most dangerous sliding surface lines of each two-dimensional profile are converted to three-dimensional slope space by using the coordinate transformation formula. Finally, the spline function interpolation is used to fit the most dangerous sliding surface lines in the three-dimensional space to construct the three-dimensional most dangerous sliding surface. Taking the southwest slope of an open-pit mine in Xilinhot, Inner Mongolia as an example, a three-dimensional engineering geological model of the slope is established, and five two-dimensional profiles for slope stability analysis are generated. Through this method, the three-dimensional most dangerous sliding surface and three-dimensional sliding mass are successfully generated and their rationality is verified.
ConclusionThe research results provide new insights for predicting the location, scale, and damage degree of potential slope sliding masses.
-
图 2 剖面空间转换关系图
m'-n'. 剖面线编号；l0，l1. 水平定位线；y0，y1，y2，y3，y4，y5. 高程定位线；h0，h1，h2，h3，h4，h5. 实际高程值；下同
Figure 2. Profile space conversion relationship diagram
图 5 自动生成多剖面最危险滑面线流程图
Figure 5. Automatically generate the flow chart of the most dangerous sliding surface line of multi-profile
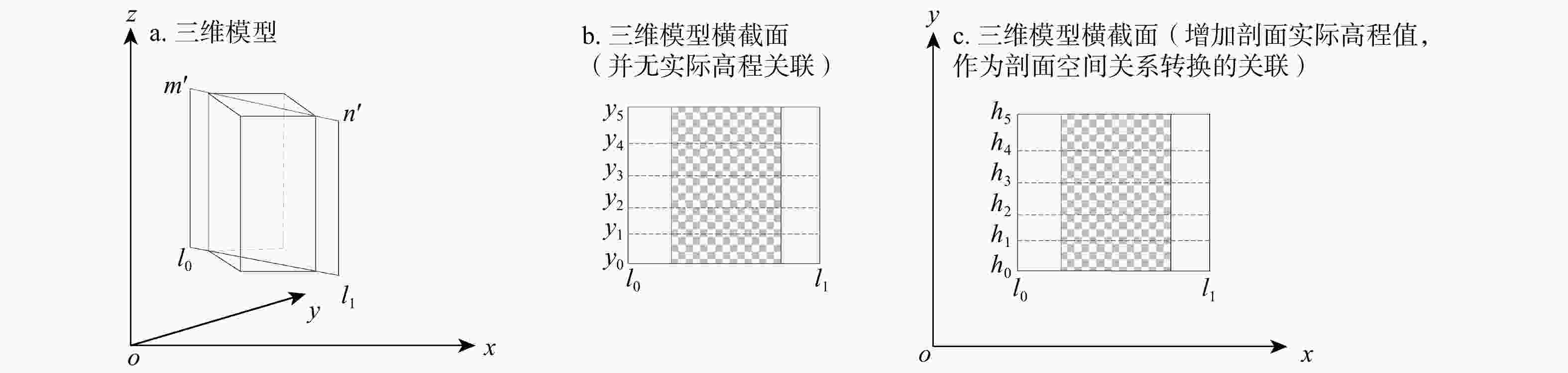
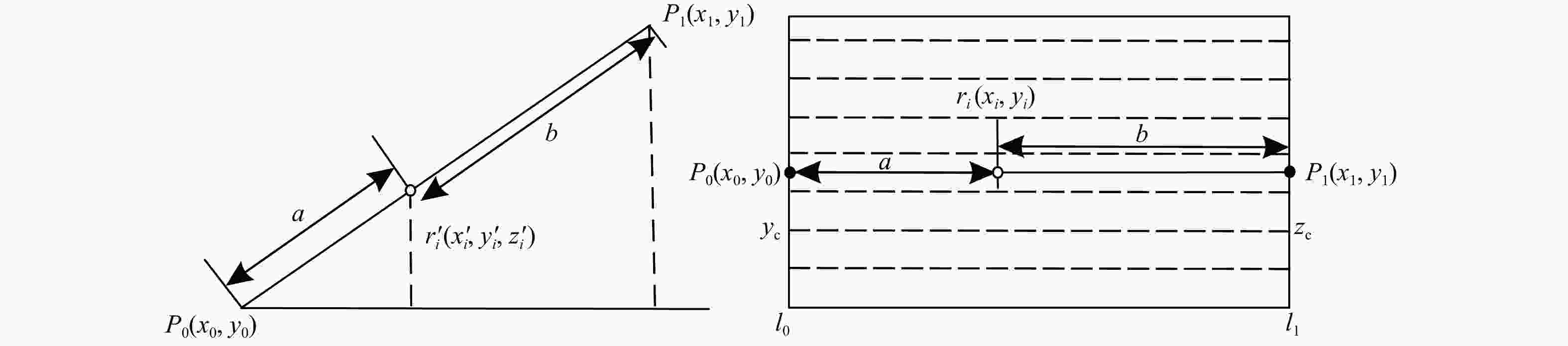
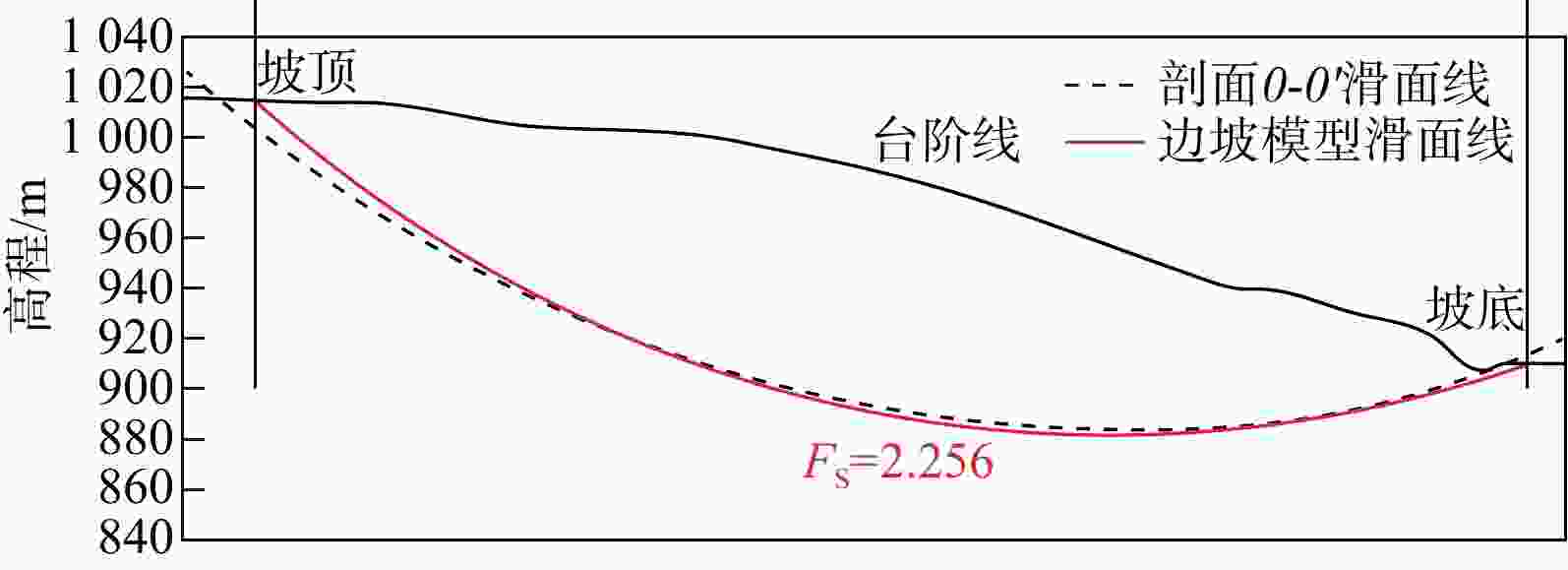
图 6 二维转三维坐标示意图
P0(x0,y0)和P1(x1,y1)为剖面线P0-P1的端点坐标，在剖面图上分别与水平定位线l0和l1对应；ri(xi, yi)为滑面线第i个顶点的二维坐标；$r_{i}{'}(x_{i}{'} , y_{i}{'} , {\textit{z}}_{i}{'}) $滑面线第i个顶点的三维坐标；$a=|x_i-x_{0}| $，$b=|x_i-x_{1}| $；yc为相应剖面图上的任意一条高程定位线的y坐标值；zc为该高程定位线的实际高程值；下同
Figure 6. Two-dimensional to three-dimensional coordinate diagram
图 8 采场现状及剖面线设计（蓝色线为剖面线，红色线为设置的坡顶和坡底范围，下同）
Figure 8. Stope status and profile lines design
图 10 1-1'剖面图及最危险滑面线
Figure 10. 1-1' profile and the most dangerous sliding surface line
图 11 三维最危险滑面线(a)和滑面(b)
Figure 11. Most dangerous sliding surface line (a) and sliding surface (b) in three-dimensional space
图 14 剖面线设置及滑面线对比
Figure 14. Setting of cross profile line and comparison between sliding surface lines
图 15 剖面0-0'与边坡模型滑面线比较
Figure 15. Comparison of sliding surface line of Profile 0-0' with slope model
表 1 岩体物理力学指标
Table 1. Physical and mechanical indexes of rock mass
地 层 岩体容重γ/(kN·m−3) 内聚力C/kPa 内摩擦角/(°) 古近系+新近系 19.3 85 24 碳质泥岩 18.3 30 14.22 砂岩 20.8 21 25.5 煤 13.9 58 26.32 泥岩 20.1 26 21.85 砂质泥岩 20.3 25.38 17.49 
下载: 导出CSV
表 2 三维滑面线数据集
Table 2. Three-dimensional sliding surface line data set
剖面名 起点坐标 中间点 终点坐标 1-1' ( 2332.570° ,3138.609° ,988.160°)...... ( 2531.391° ,3402.430° ,929.969°)2-2' ( 2520.152° ,3023.592° ,1000.597° )...... ( 2794.880° ,3227.500° ,912.907°)3-3' ( 2578.475° ,2820.756° ,1011.972° )...... ( 2956.343° ,2966.455° ,906.414°)4-4' ( 2566.577° ,2619.273° ,1016.332° )...... ( 3042.078° ,2703.763° ,900.805°)5-5' ( 2461.401° ,2374.803° ,1014.647° )...... ( 2929.546° ,2347.221° ,919.825°)6-6' ( 2390.92° ,3210.362° ,945.09°)...... ( 2603.905° ,2366.407° ,959.674°)7-7' ( 2477.535° ,3330.966° ,919.107°)...... ( 2802.998° ,2354.676° ,922.035°)
下载: 导出CSV
表 3 边坡模型与剖面0-0'滑面线误差参照
Table 3. Errors reference for sliding surface line of slope model and Profile 0-0'
高程z/m z1 中间点 zi zi+1 中间点 zn 剖面0-0' 1015.35 ...... 935.25 926.29 ...... 917.76 边坡模型 1007.07 ...... 938.12 928.07 ...... 912.09 误差 8.28 ...... −2.87 −1.78 ...... −5.67 误差率/% 0.82 ...... 0.31 0.19 ...... 0.62
下载: 导出CSV
-
[1] 陈祖煜, 弥宏亮, 汪小刚. 边坡稳定三维分析的极限平衡方法[J]. 岩土工程学报, 2001, 23(5): 525-529.CHEN Z Y, MI H L, WANG X G. A three-dimensional limit equilibrium method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 525-529. (in Chinese with English abstract [2] 吴海真, 顾冲时. 联合运用改进的极限平衡法和动态规划法分析边坡稳定性[J]. 水利学报, 2007, 38(10): 1272-1277.WU H Z, GU C S. Slope stability analysis using enhanced limit equilibrium method combined with dynamic programming[J]. Journal of Hydraulic Engineering, 2007, 38(10): 1272-1277. (in Chinese with English abstract [3] KALATEHJARI R, A RASHID A S, HAJIHASSANI M, et al. Determining the unique direction of sliding in three-dimensional slope stability analysis[J]. Engineering Geology, 2014, 182: 97-108. doi: 10.1016/j.enggeo.2014.06.002 [4] ZHOU Y D, ZOU P, WANG F F, et al. Study on high and steep slope stability and slope angle optimization of open-pit based on limit equilibrium and numerical simulation[J]. Geotechnical and Geological Engineering, 2020, 38(6): 5737-5753. doi: 10.1007/s10706-020-01390-7 [5] SU P D, QIU P, LIU B, et al. Stability prediction and optimal angle of high slope in open-pit mine based on two-dimension limit equilibrium method and three-dimension numerical simulation[J]. Physics and Chemistry of the Earth (Parts A/B/C), 2022, 127: 103151. doi: 10.1016/j.pce.2022.103151 [6] 易富, 孟兴涛, 赵文华, 等. 基于因素空间的露天采坑边坡稳定性评价[J]. 地质科技通报, 2023, 42(5): 1-9.YI F, MENG X T, ZHAO W H, et al. Evaluation of slope stability of open pit based on factor space[J]. Bulletin of Geological Science and Technology, 2023, 42(5): 1-9. (in Chinese with English abstract [7] 朱彦鹏, 杨晓宇, 马孝瑞, 等. 边坡稳定性分析双折减法的几个问题[J]. 岩土力学, 2018, 39(1): 331-338.ZHU Y P, YANG X Y, MA X R, et al. Several questions of double reduction method for slope stability analysis[J]. Rock and Soil Mechanics, 2018, 39(1): 331-338. (in Chinese with English abstract [8] 苏振宁, 邵龙潭. 基于有限元极限平衡法的三维边坡稳定性[J]. 工程科学学报, 2022, 44(12): 2048-2056.SU Z N, SHAO L T. Three-dimensional slope stability based on the finite element limit equilibrium method[J]. Chinese Journal of Engineering, 2022, 44(12): 2048-2056. (in Chinese with English abstract [9] 蒋先平, 张鹏, 卢艺伟, 等. 物质点强度折减法边坡失稳判据选择方法[J]. 地质科技通报, 2022, 41(2): 113-122.JIANG X P, ZHANG P, LU Y W, et al. Slope failure criterion for the strength reduction material point method[J]. Bulletin of Geological Science and Technology, 2022, 41(2): 113-122. (in Chinese with English abstract [10] NAEIJ M, GHASEMI H, GHAFARIAN D, et al. Explicit finite element analysis of slope stability by strength reduction[J]. Geomechanics and Engineering, 2021(2): 2. [11] 孙聪, 郑宏, 李春光, 等. 基于蚁群算法的严格最大剩余推力临界滑动面搜索[J]. 岩土力学, 2014, 35(10): 3021-3026.SUN C, ZHENG H, LI C G, et al. Critical slip surface search by using rigorous maximum residual thrust method based on ant colony algorithm[J]. Rock and Soil Mechanics, 2014, 35(10): 3021-3026. (in Chinese with English abstract [12] 杨善统, 姜清辉, 尹涛, 等. 边坡临界滑面搜索的改进粒子群优化算法[J]. 岩土工程学报, 2015, 37(8): 1411-1417.YANG S T, JIANG Q H, YIN T, et al. Search of critical slip surface of slopes using improved particle swarm optimization method[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1411-1417. (in Chinese with English abstract [13] 张锟, 徐青, 王一凡, 等. 自适应差分进化算法在边坡滑面搜索中的应用[J]. 岩土力学, 2017, 38(5): 1503-1509.ZHANG K, XU Q, WANG Y F, et al. Application of self-adaptive differential evolution algorithm in searching for critical slip surface of slope[J]. Rock and Soil Mechanics, 2017, 38(5): 1503-1509. (in Chinese with English abstract [14] 孙自立, 温树杰, 梁超, 等. 一种基于最小势能法的三维任意形滑面构造与搜索方法[J]. 岩土力学, 2020, 41(增刊1): 255-263.SUN Z L, WEN S J, LIANG C, et al. A method for constructing and searching three-dimensional arbitrary slip surface based on minimum potential energy[J]. Rock and Soil Mechanics, 2020, 41(S1): 255-263. (in Chinese with English abstract [15] CEN W J, LUO J R, YU J S, et al. Slope stability analysis using genetic simulated annealing algorithm in conjunction with finite element method[J]. KSCE Journal of Civil Engineering, 2020, 24(1): 30-37. doi: 10.1007/s12205-020-2051-5 [16] LI Y J, QIAN C, FU Z Z, et al. On two approaches to slope stability reliability assessments using the random finite element method[J]. Applied Sciences, 2019, 9(20): 4421. doi: 10.3390/app9204421 [17] 杨超, 董立山, 申俊敏, 等. 边坡矢量和分析法最危险滑面搜索研究[J]. 安全与环境工程, 2014, 21(3): 28-35.YANG C, DONG L S, SHEN J M, et al. Searching for the most dangerous failure surface of slope based on the vector sum analysis method[J]. Safety and Environmental Engineering, 2014, 21(3): 28-35. (in Chinese with English abstract [18] 吕爱钟, 贾晓阳. 边坡危险滑动面及稳定安全系数的力学解析方法[J]. 工程地质学报, 2022, 30(1): 110-116.LYU A Z, JIA X Y. Mechanical analysis method for dangerous sliding surface and factor of safety[J]. Journal of Engineering Geology, 2022, 30(1): 110-116. (in Chinese with English abstract [19] 余国, 谢谟文, 孙紫豪, 等. 基于GIS的三维对称边坡滑面正应力分布逼近函数构造[J]. 岩土力学, 2019, 40(6): 2332-2340.YU G, XIE M W, SUN Z H, et al. Construction of approximation function of normal stress distribution on sliding surface of three-dimensional symmetrical slope based on GIS[J]. Rock and Soil Mechanics, 2019, 40(6): 2332-2340. (in Chinese with English abstract [20] 郑永来, 吴卓睿. 基于最短折减路径法的边坡安全系数研究[J]. 地质科技通报, 2022, 41(6): 28-34.ZHENG Y L, WU Z R. Estimation of slope safety factor based on trajectory reduction method[J]. Bulletin of Geological Science and Technology, 2022, 41(6): 28-34. (in Chinese with English abstract [21] SHUI K, HOU K P, HOU W W, et al. Optimizing slope safety factor prediction via stacking using sparrow search algorithm for multi-layer machine learning regression models[J]. Journal of Mountain Science, 2023, 20(10): 2852-2868. doi: 10.1007/s11629-023-8158-7 [22] STIANSON J R, CHAN D, FREDLUND D G. Role of admissibility criteria in limit equilibrium slope stability methods based on finite element stresses[J]. Computers and Geotechnics, 2015, 66: 113-125. doi: 10.1016/j.compgeo.2015.01.014 [23] CAI Z L, SHOU S L, ZHOU J W, et al. System reliability analysis of landslides involving sliding surfaces using intelligent multiple response surfaces[J]. Frontiers in Earth Science, 2023, 10: 1053634. doi: 10.3389/feart.2022.1053634 [24] 曹文庚, 潘登, 徐郅杰, 等. 河南省滑坡灾害易发性制图研究: 多种机器学习模型的对比[J]. 地质科技通报: 2025, 44(1): 101-111.CAO W G, PAN D, XU Z J, et al. Landslide disaster vulnerability mapping study in Henan Province: Comparison of different machine learning models[J]. Bulletin of Geological Science and Technology: 2025, 44(1): 101-111. (in Chinese with English abstract [25] 李荣伟, 侯恩科. 露天煤矿边坡稳定性影响因素的敏感性正交分析[J]. 煤田地质与勘探, 2009, 37(1): 52-56.LI R W, HOU E K. Orthogonality analysis of sensibility on factors of slope stability in opencast coal mine[J]. Coal Geology & Exploration, 2009, 37(1): 52-56. (in Chinese with English abstract [26] 向章波, 张家铭, 周晓宇, 等. 基于Slide的某红层路堑边坡稳定性分析[J]. 水文地质工程地质, 2015, 42(4): 90-95.XIANG Z B, ZHANG J M, ZHOU X Y, et al. The slope stability analysis of red bed based on Slide[J]. Hydrogeology & Engineering Geology, 2015, 42(4): 90-95. (in Chinese with English abstract [27] 王强, 付厚利, 秦哲, 等. 基于正交改进和Geo-slope边坡稳定性因素敏感性分析[J]. 金属矿山, 2017(12): 130-135.WANG Q, FU H L, QIN Z, et al. Sensitivity analysis of slope stability factor based on orthogonal improvement and geo-slope[J]. Metal Mine, 2017(12): 130-135. (in Chinese with English abstract [28] 刘国栋, 刘奉银. 基于Geo-slope的Siegle网格密度确定问题[J]. 地下空间与工程学报, 2016, 12(2): 397-401.LIU G D, LIU F Y. Identification of the Siegel grid density within Geo-slope[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(2): 397-401. (in Chinese with English abstract [29] 李小春, 袁维, 白冰, 等. 基于局部强度折减法的边坡多滑面分析方法及应用研究[J]. 岩土力学, 2014, 35(3): 847-854.LI X C, YUAN W, BAI B, et al. Analytic approach of slope multi-slip surfaces based on local strength reduction method and its application[J]. Rock and Soil Mechanics, 2014, 35(3): 847-854. (in Chinese with English abstract [30] 张年学, 李晓, 盛祝平, 等. 多剖面合力法分析滑坡稳定性[J]. 工程地质学报, 2017, 25(5): 1190-1204.ZHANG N X, LI X, SHENG Z P, et al. Stability analysis of landslide using joint forces method on multiple profiles[J]. Journal of Engineering Geology, 2017, 25(5): 1190-1204. (in Chinese with English abstract [31] 崔扬, 李青元, 董前林, 等. 勘探线剖面图从二维转化为三维算法[J]. 测绘科学, 2016, 41(4): 128-131.CUI Y, LI Q Y, DONG Q L, et al. Research on prospecting line profile map from 2D to 3D[J]. Science of Surveying and Mapping, 2016, 41(4): 128-131. (in Chinese with English abstract -
下载:
点击查看大图
计量
- 文章访问数: 594
- PDF下载量: 80
- 被引次数: 0
