基于内外功率比的非直线坡面型边坡的稳定系数研究

程云祥; 张彤炜; 兰恒星; 张帆宇; 张虎元

doi:10.19509/j.cnki.dzkq.2022.0143

基于内外功率比的非直线坡面型边坡的稳定系数研究

doi: 10.19509/j.cnki.dzkq.2022.0143

程云祥^{1a, 1b,},
张彤炜^{1a, 1b, ,},
兰恒星^{2, 3},
张帆宇^{1a, 1b},
张虎元^{1a, 1b}

1a.
兰州大学西部灾害与环境力学教育部重点实验室, 兰州 730000
1b.
兰州大学土木工程与力学学院, 兰州 730000
2.
长安大学地质工程与测绘学院, 西安 710064
3.
中国科学院地理科学与资源研究所, 北京 100101

基金项目:

国家自然科学基金项目 42041006

国家自然科学基金项目 42090053

国家自然科学基金项目 41790443

甘肃省自然科学基金项目 20JR5RA259

中国博士后科学基金面上项目 2019M653791

中央高校基本科研业务费专项资金 lzujbky-2021-ct04

详细信息

作者简介:
程云祥(1999-), 男, 主要从事滑坡灾害模拟的研究工作。E-mail: 807565606@qq.com

通讯作者:
张彤炜(1983-), 男, 副教授, 主要从事非饱和特殊土环境灾害研究工作。E-mail: ztw@lzu.edu.cn

中图分类号: TU457
计量
- 文章访问数: 880
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2022-03-25

Stability coefficient analysis of soil slopes with non-linear topography based on the ratio of internal to external power

Cheng Yunxiang^{1a, 1b
,},
Zhang Tongwei^{1a, 1b
, ,},
Lan Hengxing^{2, 3},
Zhang Fanyu^{1a, 1b},
Zhang Huyuan^{1a, 1b}

1a.
MOE Key Laboratory of Mechanics on Disaster and Environmentin Western China, Lanzhou University, Lanzhou 730000, China
1b.
College of Civil Engineering and Mechanics, Lanzhou University, Lanzhou 730000, China
2.
School of Geological Engineering and Geomatics, Chang'an University, Xi'an 710064, China
3.
Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China

摘要

摘要:
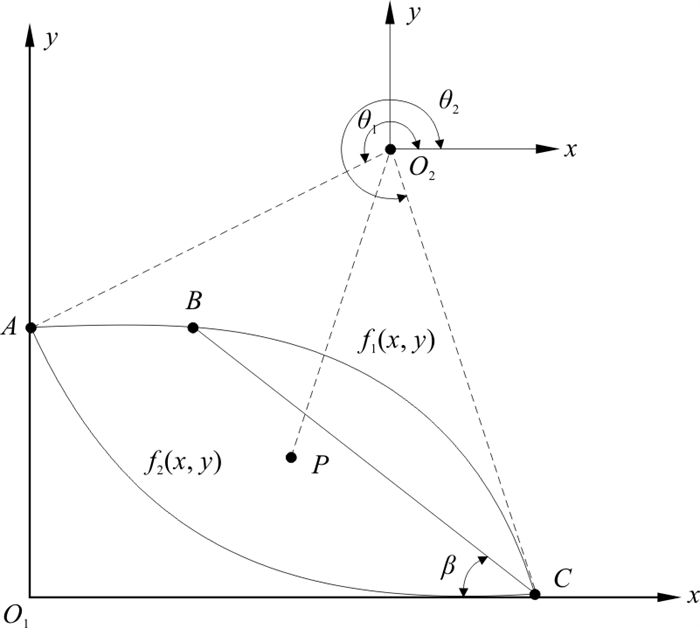
在边坡稳定性上极限分析中, 由于考虑了材料的理想弹塑性本构关系与相关流动法则, 相比极限平衡法更符合岩土材料的特征。在以往的二维边坡极限分析上限法中, 要求坡面形态为规则的直线, 而无论是天然边坡还是人工边坡, 边坡的坡面形态往往并非规则的直线。此外, 以往的边坡极限上限分析中得到的稳定数N_s=c/γH主要针对土坡的临界高度计算, 且未考虑孔压等外力对边坡施加的外功率。不同于传统极限平衡法采用静力学的平衡条件, 本研究针对非直线型坡面边坡稳定性问题, 假定滑动面为对数螺旋线, 基于极限分析上限定理和虚功原理, 提出了一种边坡发生旋转破坏时旋转中心的确定方法, 推导出了非直线型坡面边坡的重力虚功功率和能量平衡方程的解析解, 并提出了基于内、外功率之比的稳定系数K用以评价边坡的稳定性。通过算例比较了不同形态天然边坡的稳定性和人工削坡对边坡稳定性的影响, 并分析了边坡的坡度(β)、土体的内摩擦角(φ)、黏聚力(c)以及孔压系数(r_u)对稳定系数K的影响规律。对于坡度较大的边坡, 通过削坡改变坡面形态提高了边坡的稳定系数K。稳定系数K随黏聚力的增加而非线性增大, 随孔压系数的增加而降低。当黏聚力相对于孔压系数对边坡稳定性影响更大时, 稳定系数K随内摩擦角的增加而增大; 反之, 稳定系数K则随内摩擦角的增加而减小。以上结果符合对边坡稳定性分析的普遍认知, 验证了模型的合理性。另外, 通过将该方法与传统的Bishop法的计算结果进行对比, 发现安全系数F_s=1与稳定系数K=0的临界状态物理意义相同, 稳定系数K随黏聚力非线性增加, 更符合边坡的渐进破坏过程。
- 土质边坡 /
- 非直线坡面 /
- 极限上限分析 /
- 虚功功率 /
- 稳定系数
Abstract:
The limit analysis of slope stability has a relatively higher calculation efficiency and accuracy because it ignores the constitutive relation of materials. Compared to the limit equilibrium method, its assumptions are strict and realistic. In the classical upper bound limit analysis, the slope surfaces are required to be a regular straight line. However, the surfaces of natural or cutting slopes are normally nonlinear. In addition, the stability number N_s=c/γH is used to calculate the critical height of slopes without considering the external power caused by pore pressure. Different from the static equilibrium conditions adopted by the traditional limit equilibrium method, this paper aimed to evaluate the stability of slopes with nonlinear surfaces based on kinetic analysis. First, a method for determining the rotation center of landslides with nonlinear surfaces based on upper bound limit analysis and the principle of virtual work was proposed. Second, it was assumed that the sliding surface was a logarithmic helix, and the virtual work under gravity and energy equilibrium equation of slopes were established. Third, the stability coefficient K defined by the ratio of internal power to external power was proposed to evaluate the stability of the slope, and the results were compared with the Bishop method to verify its effectiveness. The influences of slope degree (β), internal friction angle (φ), cohesion (c) and pore pressure coefficient (r_u) on the stability coefficient K of different natural and cutting slopes were analyzed. The results confirmed that the stability of steep slopes would be improved by cutting. The stability coefficient K increased with increasing cohesion and decreased with increasing pore water pressure coefficient. When the impact of cohesion on the stability coefficient K was more significant than that on the pore water pressure coefficient, K increased with increasing internal friction angle (φ). In contrast, the stability coefficient K decreases with increasing internal friction angle (φ). The above results followed the general understanding of slope stability analysis, and the rationality of the model was verified. By comparing the calculation results with the Bishop method, it was found that the intension of the critical state represented by safety factor F_S=1 was the same as the stability coefficient K=0 defined in this paper. The stability coefficient K increased nonlinearly with increasing cohesion, which was in line with the progressive failure mode of the soil slopes.
- soil slope /
- non-linear topography slope /
- upper bound limit analysis /
- virtual work /
- stability coefficient

HTML全文

图 1 二维边坡旋转滑移块体的几何模型及参数示意图

Figure 1. Diagram of the geometric model and parameters of a two-dimensional slope and sliding block

下载: 全尺寸图片幻灯片

图 2 二维边坡${\dot W_\gamma }$和${\dot W_w}$推导及计算参数示意图(各参数含义见正文)

Figure 2. Diagram of the ${\dot W_\gamma }$ and ${\dot W_w}$ calculation of a two-dimensional slope

下载: 全尺寸图片幻灯片

图 3 ${\dot W_\gamma }$取值示意图(图中物理量的含义见正文)

a. ${\vec F_\gamma }$与${\vec v_\gamma }$的夹角α> $\frac{\pi }{2}$；b.${\vec F_\gamma }$与${\vec v_\gamma }$的夹角α < $\frac{\pi }{2}$

Figure 3. Diagram of the value of ${\dot W_\gamma }$

下载: 全尺寸图片幻灯片

图 4 稳定系数K计算流程图

Figure 4. Calculation processes of stability coefficient K

下载: 全尺寸图片幻灯片

图 5 算例1天然边坡示意图

Figure 5. Case 1:The sizes of natural slopes in meters

下载: 全尺寸图片幻灯片

图 6 算例2人工削坡示意图

Figure 6. Case 2:The sizes of cutting slopes in meters

下载: 全尺寸图片幻灯片

图 7 黏聚力(a)、孔压系数(b)以及坡度(c)对稳定系数K的影响

Figure 7. Effects of cohesion (a), pore pressure coefficient (b) and inclination (c) on stability coefficient K

下载: 全尺寸图片幻灯片

图 8 内摩擦角φ对稳定系数K的影响

c为黏聚力；r_u为孔压系数；β为坡度

Figure 8. Influences of internal friction angle φ on stability coefficient K

下载: 全尺寸图片幻灯片

图 9 基于内外功率比的稳定系数K与基于Bishop法的安全系数F_s计算结果对比

Figure 9. Comparison of stability coefficient K based on the ratio of internal to external power and safety factor F_s based on the Bishop method

下载: 全尺寸图片幻灯片

图 10 稳定系数K的查表确定

c为黏聚力；φ为内摩擦角；r_u为孔压系数

Figure 10. Graphical determination of the stability coefficient K

下载: 全尺寸图片幻灯片

表 1 算例1中的参数取值

Table 1. Parameters in Case 1

边坡几何参数	土体性质参数	地震影响系数	孔压系数
H=10 m l_AB=3 m β=45°	γ=15 kN/m³ φ=20° c=35 kPa	K_v=0.2 K_h=0.2	r_u=0.2

下载: 导出CSV

表 2 算例1稳定系数K计算结果

Table 2. Stability coefficient K in Case 1

坡面形态	平坡	凸坡	凹坡
K	0.289	0.169	0.401

下载: 导出CSV

表 3 算例2中的参数取值

Table 3. Parameters in Case 2

边坡几何参数	土体性质参数	地震影响系数	孔压系数
H=10 m l_AB=3 m β=73°	γ=15 kN/m³ φ=20° c=35 kPa	K_v=0.2 K_h=0.2	r_u=0.2

下载: 导出CSV

表 4 算例2稳定系数K计算结果

Table 4. Stability coefficient K in Case 2

坡面形态	原始边坡	多级削坡	单级削坡
K	0.052	0.386	0.383

下载: 导出CSV

表 5 算例3中的参数取值

Table 5. Parameters in Case 3

边坡几何参数	土体性质参数	地震影响系数	孔压系数
H=10 m l_AB=3 m β=45°	γ=18 kN/m³ φ=18°	K_v=0 K_h=0	r_u=0

下载: 导出CSV

参考文献(31)

[1]	卢操, 晏鄂川, 张瑜, 等. 降雨作用下青石镇政府后山堆积层滑坡渗流与稳定性[J]. 地质科技通报, 2020, 39(2): 139-147. doi: 10.19509/j.cnki.dzkq.2020.0215 Lu C, Yan E C, Zhang Y, et al. Seepage and stability of the colluvial landslide on the back hill of Qingshi Town Government under rainfall[J]. Bulletin of Geological Science and Technology, 2020, 39(2): 139-147(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0215
[2]	蒋先平, 张鹏, 卢艺伟, 等. 物质点强度折减法边坡失稳判据选择方法[J/OL]. 地质科技通报: 1-10(2021-10-19)[2022-04-17]https://kns.cnki.net/kcms/detail/42.1904.P.20211019.1142.006.html. Jiang X P, Zhang P, Lu Y W, et al. Slope failure criteria of material point strength reduction method[J/OL]. Bulletin of Geological Science and Technology: 1-10(2021-10-19)[2022-04-10]https://kns.cnki.net/kcms/detail/42.1904.P.20211019.1142.006.html(in Chinese with English abstract).
[3]	丁戈媛, 胡新丽. 大奔流顺层岩质滑坡溃屈型破坏力学机制研究[J]. 地质科技通报, 2020, 39(2): 186-190. doi: 10.19509/j.cnki.dzkq.2020.0220 Ding G Y, Hu X L. Mechanical mechanism of buckling failure of Dabenliu consequent bedding rockslide[J]. Bulletin of Geological Science and Technology, 2020, 39(2): 186-190(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0220
[4]	吴益平, 卢里尔, 薛阳. 基于临界状态的边坡渐进破坏力学模型分析及应用[J]. 地质科技通报, 2020, 39(5): 1-7. doi: 10.19509/j.cnki.dzkq.2020.0501 Wu Y P, Lu L E, Xue Y. Application of landslide progressive failure mechanical model based on the critical stress state[J]. Bulletin of Geological Science and Technology, 2020, 39(5): 1-7(in Chinese with English abstract). doi: 10.19509/j.cnki.dzkq.2020.0501
[5]	Sun C, Chai J, Luo T, et al. Nonlinear shear-strength reduction technique for stability analysis of uniform cohesive slopes with a general nonlinear failure criterion[J]. International Journal of Geomechanics, 2021, 21(1): 06020033. doi: 10.1061/(ASCE)GM.1943-5622.0001885
[6]	Yang Y, Wu W, Zheng H. Stability analysis of slopes using the vector sum numerical manifold method[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(1): 345-352. doi: 10.1007/s10064-020-01903-x
[7]	Firincioglu B S, Ercanoglu M. Insights and perspectives into the limit equilibrium method from 2D and 3D analyses[J]. Engineering Geology, 2021, 281: 105968. doi: 10.1016/j.enggeo.2020.105968
[8]	Su Z, Shao L. A three-dimensional slope stability analysis method based on finite element method stress analysis[J]. Engineering Geology, 2021, 280: 105910. doi: 10.1016/j.enggeo.2020.105910
[9]	饶平平, 吴健, 崔纪飞, 等. 裂缝边坡三维极限上限拓展分析[J]. 岩土工程学报, 2021, 43(9): 1612-1620. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202109008.htm Rao P P, Wu J, Cui J F, et al. Extended three-dimensional analysis of cracked slopes using upper-bound limit method[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(9): 1612-1620(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202109008.htm
[10]	杨括宇, 陈从新, 夏开宗, 等. 顺层缓倾复合介质边坡水力驱动型滑移破坏机制研究[J]. 中国公路学报, 2018, 31(2): 144-153. doi: 10.3969/j.issn.1001-7372.2018.02.015 Yang K Y, Chen C X, Xia K Z, et al. Research on sliding failure mechanism of gently inclined bedding compound rock mass slope under hydraulic drive[J]. China Journal of Highway and Transport, 2018, 31(2): 144-153(in Chinese with English abstract). doi: 10.3969/j.issn.1001-7372.2018.02.015
[11]	Chen W F. Limit analysis and soil plasticity[M]. [S. l. ]: J. Ross Publishing, 2007.
[12]	李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004. Li G X. Advanced soil mechanics[M]. Beijing: Tsinghua University Press, 2004(in Chinese).
[13]	Michalowski R L. Slope stability analysis: A kinematical approach[J]. Geotechnique, 1995, 45(2): 283-293. doi: 10.1680/geot.1995.45.2.283
[14]	Utili S, Abd A H. On the stability of fissured slopes subject to seismic action[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(5): 785-806. doi: 10.1002/nag.2498
[15]	陈祖煜. 土力学经典问题的极限分析上、下限解[J]. 岩土工程学报, 2002, 24(1): 1-11. doi: 10.3321/j.issn:1000-4548.2002.01.001 Chen Z Y. Limit analysis for the classic problems of soil mechanics[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(1): 1-11(in Chinese with English abstract). doi: 10.3321/j.issn:1000-4548.2002.01.001
[16]	王均星, 王汉辉, 吴雅峰. 土坡稳定的有限元塑性极限分析上限法研究[J]. 岩石力学与工程学报, 2004, 23(11): 1867-1873. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200411020.htm Wang J X, Wang H H, Wu Y F. Stability analysis of soil slope by finite element method with plastic limit upper bound[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(11): 1867-1873(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200411020.htm
[17]	王均星, 王汉辉, 张优秀, 等. 非均质土坡的有限元塑性极限分析[J]. 岩土力学, 2004, 25(3): 415-421. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200403017.htm Wang J X, Wang H H, ZhangY X, et al. Plastic limit analysis of heterogeneous soil slope using finite elements[J]. Rock and Soil Mechanics, 2004, 25(3): 415-421(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200403017.htm
[18]	王均星, 李泽. 考虑孔隙水压力的土坡稳定性的有限元上限分析[J]. 岩土力学, 2007, 28(2): 213-218. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200702000.htm Wang J X, Li Z. Upper bound analysis of stability of soil slope subjected to pore water pressure using finite elements[J]. Rock and Soil Mechanics, 2007, 28(2): 213-218(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200702000.htm
[19]	卢坤林, 朱大勇. 坡面形态对边坡稳定性影响的理论与试验研究[J]. 岩石力学与工程学报, 2014, 33(1): 35-42. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201401004.htm Lu K L, Zhu D Y. Theoretical and experimental study of effect of slope topography on its stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1): 35-42(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201401004.htm
[20]	陈祖煜. 建筑物抗滑稳定分析中"潘家铮最大最小原理"的证明[J]. 清华大学学报: 自然科学版, 1998, 38(1): 3-6. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB801.000.htm Chen Z Y. On Pan's principles of soil and rock stability analysis[J]. Journal of Tsinghua University: Natural Science Edition, 1998, 38(1): 3-6(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB801.000.htm
[21]	Johnson C. Existence theorem for plasticity problem[J]. Journal de Mathématiques Pures et Appliqués, 1976, 55(4): 431-444.
[22]	Donald I B, Chen Z. Slope stability analysis by the upper bound approach: Fundamentals and methods[J]. Canadian Geotechnical Journal, 1997, 34(6): 853-862.
[23]	Wai-Fah C. Limit analysis and soil plasticity[M]. Amsterdam: Elsevier, 2013.
[24]	Michalowski R L. Stability assessment of slopes with cracks using limit analysis[J]. Canadian Geotechnical Journal, 2013, 50(10): 1011-1021.
[25]	常胜利. 多边形重心坐标的求法[J]. 高等数学研究, 2005, 8(2): 21-23. https://www.cnki.com.cn/Article/CJFDTOTAL-XUSJ20050200A.htm Chang S L. A method for finding the coordinates of the gravity center of a polygon[J]. Studies in College Mathematics, 2005, 8(2): 21-23(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-XUSJ20050200A.htm
[26]	Voulgari C, Utili S. A general analytical solution for the evolution of cliffs accounting for strength degradation, seismic action, formation of tension cracks and seepage[J]. Engineering Geology, 2017, 219: 92-106.
[27]	Bishop A W, Morgenstern N. Stability coefficients for earth slopes[J]. Geotechnique, 1960, 10(4): 129-153.
[28]	Utili S. Investigation by limit analysis on the stability of slopes with cracks[J]. Geotechnique, 2013, 63(2): 140-154.
[29]	雷晓锋. 黄土边坡强度参数的选取及应用[D]. 西安: 长安大学, 2005. Lei X F. Selection and application of strength parameters of loess slope[D]. Xi'an: Chang'an University, 2005(in Chinese with English abstract).
[30]	曾洲. 花岗岩残积土地区人工边坡稳定性研究[D]. 广州: 华南理工大学, 2019. Zeng Z. Study on stability of artificial slope in granite residual area[D]. Guangzhou: South China University of Technology, 2019(in Chinese with English abstract).
[31]	卢锋, 仇文革. 基于能量演化理论的多参数非等比例折减的安全系数求解方法[J]. 岩土力学, 2021, 42(2): 547-557. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202102027.htm Lu F, Qiu W G. A multiparameter non-proportional shear strength reduction method for slope stability analysis based on energy evolution theory[J]. Rock and Soil Mechanics, 2021, 42(2): 547-557(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202102027.htm